题目内容
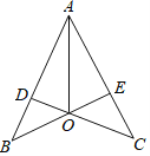
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.

【答案】(1)见解析;(2)见解析;(3)DQ=AD+DP.
【解析】
(1)由直角三角形的性质得出∠ABC=60°,由角平分线的定义得出∠A=∠DBA,证出AD=BD,由线段垂直平分线的性质得出AE=BE,由直角三角形斜边上的中线性质得出CE=![]() AB=BE,即可得出结论;
AB=BE,即可得出结论;
(2)由等边三角形的性质得出BC=BE,BM=BN,∠EBC=∠MBN=60°,证出∠CBM=∠EBN,由SAS证明△CBM≌△EBN,得出∠BEN=∠BCM=60°,得出∠BEN=∠EBC,即可得出结论;
(3)延长BD至F,使DF=PD,连接PF,证出△PDF为等边三角形,得出PF=PD=DF,∠F=∠PDQ=60°,得到∠F=∠PDQ=60°,证出∠Q=∠PBF,由AAS证明△PFB≌△PDQ,得出DQ=BF=BD+DF=BD+DP,证出AD=BD,即可得出结论.
(1)证明:∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵BD是△ABC的角平分线,
∴∠DBA=![]() ∠ABC=30°,
∠ABC=30°,
∴∠A=∠DBA,
∴AD=BD,
∵DE⊥AB,
∴AE=BE,
∴CE=![]() AB=BE,
AB=BE,
∴△BCE是等边三角形;
(2)证明:∵△BCE与△MNB都是等边三角形,
∴BC=BE,BM=BN,∠EBC=∠MBN=60°,
∴∠CBM=∠EBN,
在△CBM和△EBN中,

∴△CBM≌△EBN(SAS),
∴∠BEN=∠BCM=60°,
∴∠BEN=∠EBC,
∴EN∥BC;
(3)解:DQ=AD+DP;理由如下:
延长BD至F,使DF=PD,连接PF,如图所示:
∵∠PDF=∠BDC=∠A+∠DBA=30°+30°=60°,
∴△PDF为等边三角形,
∴PF=PD=DF,∠F=60°,
∵∠PDQ=90°-∠A=60°,
∴∠F=∠PDQ=60°,
∴∠BDQ=180°-∠BDC-∠PDQ=60°,
∴∠BPQ=∠BDQ=60°,
∴∠Q=∠PBF,
在△PFB和△PDQ中,

∴△PFB≌△PDQ,
∴DQ=BF=BD+DF=BD+DP,
∵∠A=∠ABD,
∴AD=BD,
∴DQ=AD+DP.