题目内容
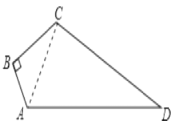
【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积为______。
【答案】36
【解析】
连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
连接AC，如图所示：
∵∠B=90°，
∴△ABC为直角三角形，
又∵AB=3，BC=4，
∴根据勾股定理得：AC=
=5，
又∵CD=12，AD=13，
∴AD
=13=169,CD+AC=12+5=144+25=169，
∴CD+AC=AD，
∴△ACD为直角三角形,∠ACD=90°，
则S四边形ABCD=S△ABC+S△ACD=
ABBC+ACCD=×3×4+×5×12=36，
故四边形ABCD的面积是36
练习册系列答案
相关题目
【题目】有20筐橘子，以每筐20千克为标准，超过或不足的部分分别用正数或负数来表示，记录如下：
与标准重量的差(单位：千克) | －2 | －1.5 | －1 | 0 | 1 | 1.5 |
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)求最重的一筐比最轻的一筐重多少？
(2)求20筐橘子的总重量是多少千克？
【题目】某部队新兵入伍时，对新兵进行“引体向上”测试，以50次为标准，超过50次用正数表示，不足50次用负数表示，第二小队的10名新兵的成绩如下表：
3 |
| 0 | 8 | 7 |
| 10 | 1 |
| 5 |
（1）求第二小队的总成绩；
（2）求第二小队的平均成绩。
