��Ŀ����
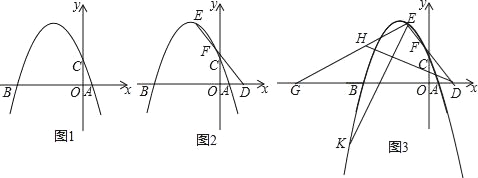
����Ŀ����ͼ1����֪������y=��![]() x2��
x2��![]() x+c��x���ཻ��A��B���㣨B����A�����ࣩ����y���ཻ��C�㣬��AB=10��
x+c��x���ཻ��A��B���㣨B����A�����ࣩ����y���ཻ��C�㣬��AB=10��
��1�������������ߵĽ���ʽ��
��2����ͼ2��D����x���ϣ�����A����Ҳ࣬E��Ϊ�������ϵڶ������ڵĵ㣬����ED���������ڵڶ������ڵ�����һ��F����E��y��ľ������F��y��ľ���֮��Ϊ3��1����֪tan��BDE=![]() �����E�����ꣻ
�����E�����ꣻ
��3����ͼ3���ڣ�2���������£���G��B��������x�Ḻ�����˶�������EG����H���߶�EG�ϣ�����DH����EDH=��EGB������E��EK��DH������������Ӧ��E����EK=EG�����K�����꣮
���𰸡���1��y=��![]() x2��
x2��![]() x+3����2��E����3��8������3��K(-11��-8).
x+3����2��E����3��8������3��K(-11��-8).
�������������������1���ȸ��ݺ�����ϵʽ����Գ��ᣬ��AB=10���������![]() �����꣬���뺯����ϵʽ���
�����꣬���뺯����ϵʽ���![]() ��ֵ�����ɽ��
��ֵ�����ɽ��
��2����EM��x�ᣬ����Ϊ��M��FN��x�ᣬ����Ϊ��N��FT��EM������Ϊ��T.�õ��ı���FTMNΪ���Σ���![]() ,
, ![]() ,�õ���BDE=��EFT������
,�õ���BDE=��EFT������![]() ����
����![]() �õ�
�õ�![]() ����
����![]() ���
���![]() ���뺯����ϵʽ���ɽ��
���뺯����ϵʽ���ɽ��
��3����EM��x�ᣬ����Ϊ��M������K��KR��ED����ED�ཻ�ڵ�R����x���ཻ�ڵ�Q.��֤�����EGM�ա�EKR�����![]()
![]() ֱ��RQ�Ľ���ʽΪ��
ֱ��RQ�Ľ���ʽΪ�� ![]() ���K������Ϊ
���K������Ϊ![]() ���������߽���ʽ�ɵ�x=11,�����ɽ��
���������߽���ʽ�ɵ�x=11,�����ɽ��
���������(1)��![]()
�ɵöԳ���Ϊx=4
��AB=10��
���A������Ϊ(1,0)��
![]() ��c=3
��c=3
�������ߵĽ���ʽΪ![]()
(2)��ͼ2����EM��x�ᣬ����Ϊ��M��FN��x�ᣬ����Ϊ��N��FT��EM������Ϊ��T.
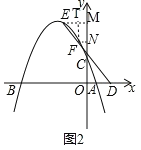
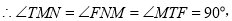
���ı���FTMNΪ���Σ�
��![]() ,
, ![]() ,
,
���BDE=��EFT��
![]()
![]()
��![]()
![]()
��![]() ����E.F��
����E.F��
��![]()
���m=0(��ȥ)��m=1��
��m=1ʱ��3m=3��
![]()
��E(3,8).
(3)��ͼ3����EM��x�ᣬ����Ϊ��M������K��KR��ED����ED�ཻ�ڵ�R����x���ཻ�ڵ�Q.

![]()
���KER=��GEM��
�ڡ�EGM�͡�EKR�У�
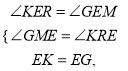
���EGM�ա�EKR��
��EM=ER=8��
![]()
��ED=10��
��DR=2��
![]()
![]() ����
����![]()
��ֱ��RQ�Ľ���ʽΪ�� ![]() ���K������Ϊ
���K������Ϊ![]() �����������߽���ʽ�ɵ�x=11,
�����������߽���ʽ�ɵ�x=11,
��K(11,8).