题目内容
【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

【答案】(1)t=2min;(2)①甲登山上升的速度是10m/min;y=10x+100(0≤x≤20);x=3,10,13
【解析】试题分析:(1)根据速度=高度÷时间即可算出甲登山上升的速度,即可算出乙在A地时所用的时间![]()
![]() ①求得乙提速后乙的速度,根据乙登山的上升速度是甲登山的上升速度3倍,即可求得甲的速度.
①求得乙提速后乙的速度,根据乙登山的上升速度是甲登山的上升速度3倍,即可求得甲的速度.
②找出甲登山全程中y关于x的函数关系式.
③分![]() 和
和![]() 两种情况,根据高度=初始高度+速度×时间即可得出乙登上过程中y关于x的函数关系;令二者做差等于70即可得出关于x的一元一次方程,解之即可得出结论.
两种情况,根据高度=初始高度+速度×时间即可得出乙登上过程中y关于x的函数关系;令二者做差等于70即可得出关于x的一元一次方程,解之即可得出结论.
试题解析:
(1)![]() 解得:
解得: ![]()
故答案为:2.
(2)①乙提速后,乙的登上速度为: ![]()
乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
甲登山上升的速度是10m/min;
故答案为:10.
∵甲登山上升的速度是10m/min,
∴甲登山所用的时间为20min.
即点![]()
由图像可知点![]()
设直线CD的函数关系式: ![]()
③当![]() 时,
时, ![]()
![]() 时,y=30+10×3(x2)=30x30.
时,y=30+10×3(x2)=30x30.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为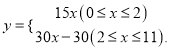
(3)当10x+100(30x30)=70时,解得:x=3;
当30x30(10x+100)=70时,解得:x=10.
当![]() 时,解得:x=13.
时,解得:x=13.
答:登山3分钟或10分钟或13分钟时,甲、乙两人距地面的高度差为70米.