题目内容
【题目】已知![]() ,点
,点![]() 分别在射线
分别在射线![]() 上运动(不与点
上运动(不与点![]() 重合)
重合)
观察:
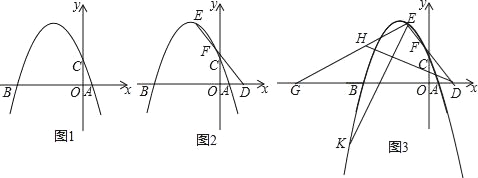
(1)如图1,若![]() 和
和![]() 的平分线交于点
的平分线交于点![]() ,
,![]() _____°
_____°

猜想:
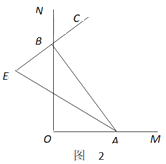
(2)如图2,随着点![]() 分别在射线
分别在射线![]() 上运动(不与点
上运动(不与点![]() 重合). 若
重合). 若![]() 是
是![]() 的平分线,
的平分线,![]() 的反向延长线与
的反向延长线与![]() 的平分线交于点
的平分线交于点![]() ,
, ![]() 的大小会变吗?如果不会,求
的大小会变吗?如果不会,求![]() 的度数;如果会改变,说明理由.
的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在四边形
落在四边形![]() 内点
内点![]() ′的位置,求
′的位置,求![]() 的度数.
的度数.

【答案】(1)135°;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1) 由三角形内角和定理得出∠OBA+∠OAB=90°,由角平分线的性质定理得出∠ABC+∠BAC=![]() ×90°=45°,再由三角形内角和定理即可得出结果;
×90°=45°,再由三角形内角和定理即可得出结果;
(2)根据∠BAO和∠ABN的平分线以及△ABO的外角的性质求解即可得到∠E的值不变;
(3)根据折叠可得,![]() ,
,![]() ,依据平角的意义得
,依据平角的意义得![]() ,
,![]() ,结合(2)的结论通过计算即可得到结果.
,结合(2)的结论通过计算即可得到结果.
(1) ∵∠MON=90°,
∴∠OBA+∠OAB=90°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC=![]() ×90°=45°,
×90°=45°,
∴∠ACB=180°-45°=135°;
(2)∵![]() 是
是![]() 的平分线
的平分线
∴![]()
∵![]() 是
是![]() 的平分线
的平分线
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
即![]()
拓展:
(3)由折叠可得,![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∵![]() ,
,![]()
∴![]()
![]()
![]()
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目