题目内容
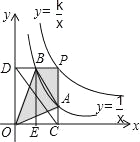
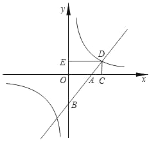
【题目】如图,直线y=x+b交x轴于A点,交y轴于B点,与反比例函数y= ![]() 交于点D,作DC⊥x轴,DE⊥y轴,则ADBD的值为________.
交于点D,作DC⊥x轴,DE⊥y轴,则ADBD的值为________.
【答案】4
【解析】
设D(x,y),由一次函数的性质知∠ABO=45°,从而AD=![]() OE,BD=
OE,BD=![]() BE,ADBD=2OEBE=2(y2﹣by),联立一次函数和反比例函数解析式可求y2﹣yb=2,进而可求出结论.
BE,ADBD=2OEBE=2(y2﹣by),联立一次函数和反比例函数解析式可求y2﹣yb=2,进而可求出结论.
解:设D(x,y)
∴OE=y,
∵y=x+b中,k=1,
∴∠ABO=45°,
∴∠OAB=45°,
∴AD=![]() OE,BD=
OE,BD=![]() BE,
BE,
∴ADBD=2OEBE,
∵令x=0代入y=x+b,
∴y=b,
∴B(0,b),
∴BE=y﹣b,
∴ADBD=2y(y﹣b)=2(y2﹣by),
∵点D在直线y=x+b与y=![]() 上,
上,
∴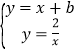 .
.
∴y2﹣yb=2,
∴ADBD=2×2=4,
故答案为4.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.