题目内容
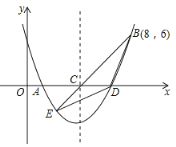
【题目】如图,直线 ![]() 与x轴,y轴分别交于A,B两点,在y轴上有一点
与x轴,y轴分别交于A,B两点,在y轴上有一点![]() ,动点M从点A以每秒1个单位的速度沿x轴向左移动.
,动点M从点A以每秒1个单位的速度沿x轴向左移动.

(1)求A,B两点的坐标;
(2)求![]() 的面积S与动点M的移动时间t(秒)之间的函数关系式;
的面积S与动点M的移动时间t(秒)之间的函数关系式;
(3)当t为何值时![]() ?并求此时点M的坐标.
?并求此时点M的坐标.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)t的值为2或6时,
;(3)t的值为2或6时,![]() ,点M的坐标是
,点M的坐标是![]() 或
或![]() .
.
【解析】
(1)由直线![]() 的函数解析式,令
的函数解析式,令![]() 求
求![]() 点坐标,
点坐标,![]() 求
求![]() 点坐标;
点坐标;
(2)由面积公式![]() 求出
求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若![]() ,
,![]() ,则
,则![]() 时间内移动了
时间内移动了![]() ,可算出
,可算出![]() 值,并得到
值,并得到![]() 点坐标.
点坐标.
(1)对于直线![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
则A,B两点的坐标分别为![]()
![]() .
.
(2)![]()
![]()
![]() .
.
当![]() 时,
时,![]() ,
,
![]() ;
;
当![]() 时,
时,![]() ,
,
![]() .
.
综上所述,S与t之间的函数关系式为
![]() .
.
(3)分为两种情况:①当M在OA上时,
![]()
![]() .
.
![]() .
.
此时![]() ,点M的坐标为
,点M的坐标为![]() ;
;
②当M在AO的延长线上时,![]()
![]() .
.
此时![]() ,点M的坐标为
,点M的坐标为![]() .
.
即t的值为2或6时,![]() ,
,
点M的坐标是![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm