题目内容
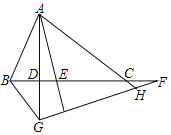
【题目】如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DAE=∠F;②∠DAE=![]() (∠ABD﹣∠ACE);③S△AEB:S△AEC=AB:AC;④∠AGH=∠BAE+∠ACB,其中正确的结论有( )个.
(∠ABD﹣∠ACE);③S△AEB:S△AEC=AB:AC;④∠AGH=∠BAE+∠ACB,其中正确的结论有( )个.
A.1B.2C.3D.4
【答案】D
【解析】
如图,①根据三角形的内角和即可得到∠DAE=∠F;②根据角平分线的定义得∠EAC=![]() ,由三角形的内角和定理得∠DAE=90°﹣∠AED,变形可得结论;③根据三角形的面积公式即可得到S△AEB:S△AEC=AB:CA;④根据三角形的内角和和外角的性质即刻得到∠AGH=∠BAE+∠ACB.
,由三角形的内角和定理得∠DAE=90°﹣∠AED,变形可得结论;③根据三角形的面积公式即可得到S△AEB:S△AEC=AB:CA;④根据三角形的内角和和外角的性质即刻得到∠AGH=∠BAE+∠ACB.
解:如图,AE交GF于M,
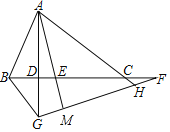
①∵AD⊥BC,FG⊥AE,
∴∠ADE=∠AMF=90°,
∵∠AED=∠MEF,
∴∠DAE=∠F;故①正确;
②∵AE平分∠BAC交BC于E,
∴∠EAC=![]() ,
,
∠DAE=90°﹣∠AED,
=90°﹣(∠ACE+∠EAC),
=90°﹣(∠ACE+![]() ),
),
=![]() (180°﹣2∠ACE﹣∠BAC),
(180°﹣2∠ACE﹣∠BAC),
=![]() (∠ABD﹣∠ACE),
(∠ABD﹣∠ACE),
故②正确;
③∵AE平分∠BAC交BC于E,
∴点E到AB和AC的距离相等,
∴S△AEB:S△AEC=AB:CA;故③正确,
④∵∠DAE=∠F,∠FDG=∠FME=90°,
∴∠AGH=∠MEF,
∵∠MEF=∠CAE+∠ACB,
∴∠AGH=∠CAE+∠ACB,
∴∠AGH=∠BAE+∠ACB;故④正确;
故选:D.

【题目】为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射击成绩折线统计图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?