题目内容
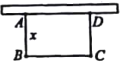
【题目】如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m)。
设花圃的面积为![]() AB的长为xm.
AB的长为xm.
(1)求y与x函数关系式,并写出x的取值范围;
(2)x为何值时,y取得最大值?最大值是多少?
【答案】(1) y=-2x2+24x; 2≤x<12;(2)x=6时,y有最大值72.
【解析】
(1)AB的长为xm,则平行于墙的一边长为(24-2x)m,该花圃的面积为[(24-2x)x]m2;进而得出函数关系即可;
(2)根据二次函数的性质即可求出最大值.
解:(1)y=(24-2x)x=24x-2x2=-2x2+24x;
又∵x>0,且20≥24-2x>0,
∴2≤x<12;
(2)y=-2x2+24x
=-2 (x2-12x+36)+72
=-2(x-6)2+72,
∵-2<0,对称轴x=6,
∴开口向下,有最大值,顶点坐标为(6,72),
∴当x=6时,y的值最大,最大值y=72.
故答案为:(1) y=-2x2+24x; 2≤x<12;(2)x=6时,y有最大值72.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射击成绩折线统计图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?