题目内容
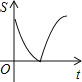
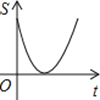
【题目】一列快车由甲地开往乙地，一列慢车由乙地开往甲地，两车同时出发，沿同一条道路匀速行驶．设行驶时间为t小时，两车之间的距离为s千米，图中折线A－B－C－D表示s与t之间的函数关系．
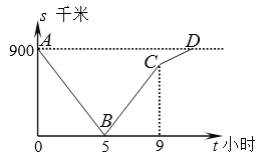
（1）求快车速度．
（2）当快车到达乙地时，慢车还要多少时间才能到达甲地．
【答案】（1）100千米/小时;（2）2.25小时
【解析】
（1）由图像可知快车9小时行驶900千米，利用路程÷时间＝速度，就可求出快车的速度.
（2）由图像可知5小时两车相遇，即5小时两车行驶900千米，可求出它们的速度和为900÷5，据此可求出慢车的速度，然后可求出当快车到达乙地时，慢车到达甲地还要的时间.
（1）解：由图可知快车的速度为：
900÷9＝100，
∴快车的速度为100千米/小时；
（2）解：慢车的速度为900÷5－100＝80千米/小时，
∴900÷80－9＝2.25小时.
当快车到达乙地时，慢车还要2.25小时才能到达甲地.
名师指导期末冲刺卷系列答案
【题目】“精准扶贫”是巩固温饱成果，加快脱贫致富步伐，实现中华民族伟大复兴“中国梦”的重要保障．某驻村帮扶小组因地制宜，积极筹集资金帮助所驻村建起了一个民族工艺品加工厂．现在，工厂计划加工1000件
、
两种工艺品，现有生产这两种工艺品所需的甲种材料445米，乙种材料510米，每生产1件工艺品和1件工艺品所需甲、乙两种材料及生产成本、利润如下表：
甲材料（单位：米） | 乙材料（单位：米） | 生产成本（单位：元） | 利润（单位：元） | |
| 0.4 | 0.6 | 60 | 25 |
| 0.5 | 0.3 | 45 | 20 |
设生产种工艺品
件，1000件、两种工艺品销售完的总利润为
元，根据上述信息，解答下列问题：
（1）求与的函数解析式（也称关系式），并直接写出的取值范围；
（2）若要使加工成本不超过53400元，则有几种加工方案？那种方案的利润最大？最大利润是多少？
