��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�������y![]() bx+c��������A��1��3����B��0��1��������A��x���ƽ���߽�����������һ��C
bx+c��������A��1��3����B��0��1��������A��x���ƽ���߽�����������һ��C
��1���������ߵı���ʽ���䶥�����ꣻ
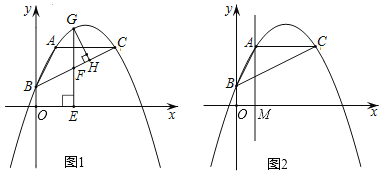
��2����ͼ1����G��BC�Ϸ��������ϵ�һ�����㣬�ֱ����G��GH��BC�ڵ�H����GE��x���ڵ�E����BC�ڵ�F���ڵ�G�˶��Ĺ����У���GFH���ܳ��Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3����ͼ2����A���ֱ�ߴ�ֱx���ڵ�M����NΪֱ��AM������һ�㣬����BCNΪֱ��������ʱ����ֱ��д����N�����꣮
���𰸡���1��![]() ,
,![]() ����2��������;��3����1��0����1��4����1����1����1��9��.
����2��������;��3����1��0����1��4����1����1����1��9��.
��������
��1�����ɴ���ϵ����������⣻
��2���������������C��4��3�����ó�ֱ��BC�ķ���Ϊy=![]() x+1�����BC=2
x+1�����BC=2![]() ���ָ�����BCI�ס�FGH�ó���BCI=��FGH���Ӷ�tan��BCI=tan��FGH=
���ָ�����BCI�ס�FGH�ó���BCI=��FGH���Ӷ�tan��BCI=tan��FGH=![]() ��G(x��
��G(x��![]() x2+
x2+![]() x+1)����F(x��
x+1)����F(x��![]() x+1)�ó�GF=
x+1)�ó�GF=![]() (x2)2+2�����Կɵõ�x=2ʱ��GF�����ʱ��GFH�ܳ���������Ʊȼ����к��������ʼ��������GFH���ܳ�Ϊ��GF+FH+GH=2+
(x2)2+2�����Կɵõ�x=2ʱ��GF�����ʱ��GFH�ܳ���������Ʊȼ����к��������ʼ��������GFH���ܳ�Ϊ��GF+FH+GH=2+![]() +2��
+2��
��3����N��1��n������֪B��0��1����C��4��3�������BN2=12+��n-1��2=n2-2n+2��CN2=32+��n-3��2=n2-6n+18��BC2=42+22=20���������Կ����ۣ�����BNC=90��ʱ��BN2+CN2=BC2����n1=0��n2=4������CBN=90��ʱ��BN2+BC2=CN2����n3=-1����BCN=90��ʱ��BC2+CN2=BN2����n4=9����N�������Ϊ����1��0����1��4����1��-1����1��9����
��1����������y![]() bx+c��������A��1��3����B��0��1����
bx+c��������A��1��3����B��0��1����
��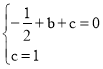 ��ã�
��ã�![]() ��c=1
��c=1
�������ߵı���ʽΪ��![]()
��![]() ��
��![]()
�ඥ������Ϊ��![]() ��
��
��2����A��1��3�������y=3����![]() ���ɵ�x1=1��x��2=4
���ɵ�x1=1��x��2=4
��C��4��3��
��B��0��1����C��4��3��
��ֱ��BC�ı���ʽΪ![]() ��BC
��BC![]()
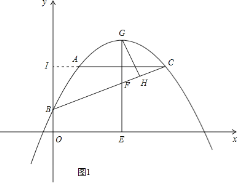
�ӳ�CA��y�ύ�ڵ�I����I��0��3��
�ߵ�G��BC�Ϸ��������ϵ�һ�����㣬�ֱ����G��GH��BC�ڵ�H����GE��x���ڵ�E����BC�ڵ�F��
���BCI�ס�FGH
���BCI=��FGH
��tan��BCI![]() ��
��
��tan��FGH![]()
��![]() ����
����![]()
��GF![]()
�൱x=2ʱ��GF�����ʱ��GFH�ܳ����
��GF=2
��![]()
��![]()
��GH![]()
��GFH���ܳ�Ϊ��GF+FH+GH=2![]() 2��
2��
��3����ͼ2�������⣬��N��1��n��
��B��0��1����C��4��3��
��BN2=12+��n��1��2=n2��2n+2��
CN2=32+��n��3��2=n2��6n+18��
BC2=42+22=20
����BNC=90��ʱ��BN2+CN2=BC2������n2��2n+2��+��n2��6n+18��=20
��n1=0��n2=4��
����CBN=90��ʱ��BN2+BC2=CN2������n2��2n+2��+20=n2��6n+18
��n3=��1
����BCN=90��ʱ��BC2+CN2=BN2����20+n2��6n+18=n2��2n+2
��n4=9
����������N�����������1��0����1��4����1����1����1��9��

 ����ͬ�����Ծ�ϵ�д�
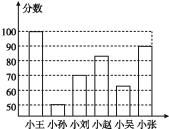
����ͬ�����Ծ�ϵ�д�����Ŀ����ʮ����У���������������ݱ�Ľ��У���У���꼶��֯1500��ѧ���μ���һ������һ��У֪ʶ�����������������в���ѧ���ijɼ���������60�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������������ѧ���ijɼ���Ϊ�������ɼ����£�
90��92��81��82��78��95��86��88��72��66��62��68��89��86��93��97��100��73��76��80��77��81��86��89��82��85��71��68��74��98��90��97��100��84��87��73��65��92��96��60��
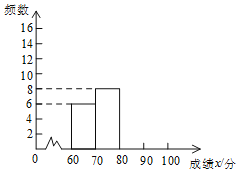
�������ɼ��������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
60��x��70 | 6 | 0.15 |
70��x��80 | 8 | 0.2 |
80��x��90 | a | b |
90��x��100 | c | d |
�����������Ϣ������������⣺
��1��a���� ����b���� ����c���� ����d���� ����
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�����ɼ���90�����ϣ�����90�֣���Ϊ�������ȣ�������Ʋμ���α�����1500��ѧ���гɼ��������ȵ�Լ�ж����ˣ�
����Ŀ��ijУΪ�˽�ѧ�������Ķ��������ѧ��ÿ���Ķ�ʱ����������˲���ѧ�������������Ա��������£�
Ů���Ķ�ʱ������ͳ�Ʊ�
�Ķ�ʱ�� | ���� | ռŮ�������ٷֱ� |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
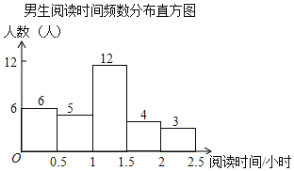
����ͼ������������⣺
��1����Ů���Ķ�ʱ������ͳ�Ʊ��У�![]() �� ��
�� ��![]() �� ��
�� ��
��2���˴γ��������У�����ȡ���� ��ѧ����ѧ���Ķ�ʱ�����λ������ ʱ��Σ�
��3�����Ķ�ʱ����2��2.5Сʱ��5��ѧ���������ȡ2��ѧ���μ��м��Ķ����ǡ�ó鵽��Ů����һ���ĸ����Ƕ��٣�