题目内容
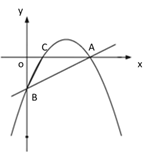
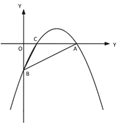
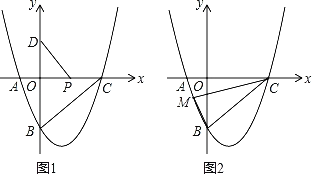
【题目】二次函数y=ax2﹣2x+c的图象与x轴交于A、C两点,点C(3,0),与y轴交于点B(0,﹣3).
(1)a= ,c= ;
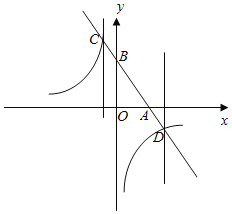
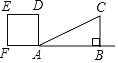
(2)如图1,P是x轴上一动点,点D(0,1)在y轴上,连接PD,求![]() PD+PC的最小值;
PD+PC的最小值;
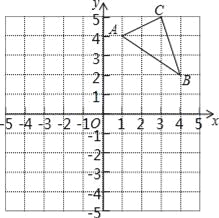
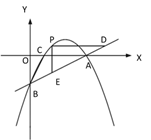
(3)如图2,点M在抛物线上,若S△MBC=3,求点M的坐标.
【答案】(1)a=1,c=﹣3;(2)4;(3)M的坐标为∴M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(1.﹣4),M4(2,﹣3).
),M3(1.﹣4),M4(2,﹣3).
【解析】
(1)利用待定系数法把问题转化为方程组即可求出答案;
(2)如图1中,作PH⊥BC于H.由![]() DP+PC=
DP+PC=![]() (PD+
(PD+![]() PC)=
PC)=![]() (PD+PH),根据垂线段最短可知,当D、P、H共线时
(PD+PH),根据垂线段最短可知,当D、P、H共线时![]() DP+PC最小,最小值为
DP+PC最小,最小值为![]() DH′;
DH′;
(3)如图2中,取点E(1,0),作EG⊥BC于G,易知EG=![]() .由S△EBC=
.由S△EBC=![]() BCEG=
BCEG=![]() 3
3![]()
![]() =3,推出过点E作BC的平行线交抛物线于M1,M2,则
=3,推出过点E作BC的平行线交抛物线于M1,M2,则![]() ,
,![]() ,求出直线M1M2的解析式,利用方程组即可解决问题,同法求出M3,M4的坐标.
,求出直线M1M2的解析式,利用方程组即可解决问题,同法求出M3,M4的坐标.
(1)把C(3,0),B(0,﹣3)代入y=ax2﹣2x+c
得到,![]() ,解得
,解得![]() .
.
故答案为1,﹣3.
(2)如图1中,作PH⊥BC
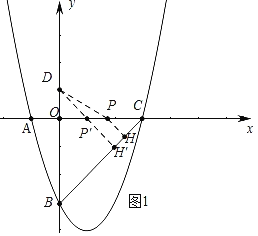
∵OB=OC=3,∠BOC=90°,
∴∠PCH=45°,
在Rt△PCH中,PH=![]() PC.
PC.
∵![]() DP+PC=
DP+PC=![]() (PD+
(PD+![]() PC)=
PC)=![]() (PD+PH),
(PD+PH),
根据垂线段最短可知,当D、P、H共线时![]() DP+PC最小,最小值为
DP+PC最小,最小值为![]() DH′,
DH′,
在Rt△DH′B中,∵BD=4,∠DBH′=45°,
∴DH′=![]() BD=2
BD=2![]() ,
,
∴![]() DP+PC的最小值为
DP+PC的最小值为![]() 2
2![]() =4.
=4.
(3)如图2中,取点E(1,0),作EG⊥BC于G,易知EG=![]() .
.
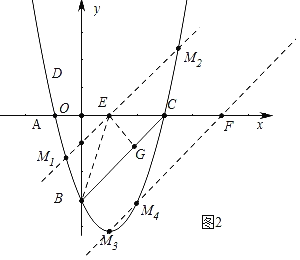
∵S△EBC=![]() BCEG=
BCEG=![]() 3
3![]()
![]() =3,
=3,
∴过点E作BC的平行线交抛物线于M1,M2,则![]() ,
,![]() ,
,
∵直线BC的解析式为y=x﹣3,
由![]() 解得
解得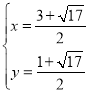 或
或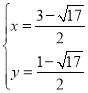 ,
,
∴M1![]() ,M2
,M2![]() ,
,
根据对称性可知,直线M1M2关于直线BC的对称的直线与抛物线的交点M3、M4也满足条件,
易知直线M3M4的解析式为y=x﹣5,
由![]() 解得
解得![]() 或
或![]() ,
,
∴M3(1.﹣4),M4(2,﹣3),
综上所述,满足条件的点M的坐标为∴M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(1.﹣4),M4(2,﹣3).
),M3(1.﹣4),M4(2,﹣3).

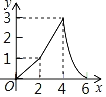
【题目】经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表.
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 6 | 2.9 | 2 | 1.5 | 1.2 | 1 |
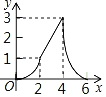
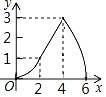
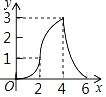
(1)请画出相应函数的图象,并求出函数表达式.
(2)点A(x1,y1),B(x2,y2)在此函数图象上.若x1<x2,则y1,y2有怎样的大小关系?请说明理由.