题目内容
【题目】定义:在三角形中,若有两条中线互相垂直,则称该三角形为中垂三角形.
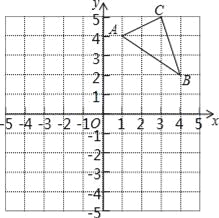
(1)如图(1),![]() 是中垂三角形,
是中垂三角形,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的中线,且
边上的中线,且![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() 是等腰三角形.
是等腰三角形.
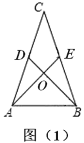


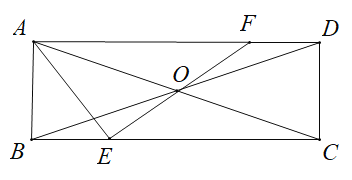
(2)如图(2),在中垂三角形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的中线,且
上的中线,且![]() 于点
于点![]() ,猜想
,猜想![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
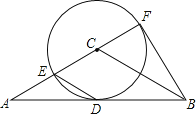
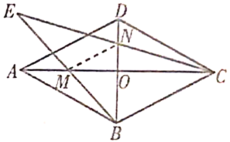
(3)如图(3),四边形![]() 是菱形,对角线
是菱形,对角线![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 并延长,交于点
并延长,交于点![]() .
.
①求证:![]() 是中垂三角形;
是中垂三角形;
②若![]() ,请直接写出
,请直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .证明见解析;(3)①见解析;②40.
.证明见解析;(3)①见解析;②40.
【解析】
(1)连接DE,根据三角形中位线定理可得![]() ,继而
,继而![]() ,由等角对等边可得
,由等角对等边可得![]() ,
,![]() 可得根据全等三角形的判定方法可证得
可得根据全等三角形的判定方法可证得![]() ,进而可得
,进而可得![]() ,由题意可得
,由题意可得![]() ,最后由等边对等角即可证得结论;
,最后由等边对等角即可证得结论;
(2)如图,连接![]() ,由中位线定理可得
,由中位线定理可得![]() ,
,![]() ,
,![]() ,再列式由勾股定理、等量代换即可求证;
,再列式由勾股定理、等量代换即可求证;
(3)①先证得MN是△AOD的中位线,再根据菱形的性质可得:CM⊥BN,AD∥BC且AD=BC,继而可得![]() ,
,![]() ,继而即可求证结论;
,继而即可求证结论;
②根据菱形的性质可得:BC=AB,再由题(2)的结论可得, ![]() 代入数值即可求解.
代入数值即可求解.
(1)证明:∵![]() ,
,![]() ,
,![]() .
.
连接![]() ,由题意可得
,由题意可得![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形.
是等腰三角形.
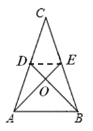
(2)![]() .
.
证明:如图,连接![]() ,
,
∵![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的中线,
上的中线,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]()
![]() .
.
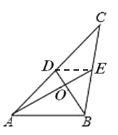
(3)①证明:如图,连接![]() .
.
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,
的中位线,
则![]() ,且
,且![]() .
.
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
从而易得![]() ,
,![]() ,
,
∴![]() ,
,![]() 是
是![]() 的中线,
的中线,
∴![]() 是中垂三角形.
是中垂三角形.
②40.
由(2)易得![]() .
.

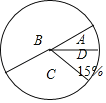
【题目】某市将开展演讲比赛活动,某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计,绘制了如下不完整的统计表和扇形统计图,
成绩等级 | 频数 | 频率 |
A | 4 | n |
B | m | 0.51 |
C | ||
D | 15 |
(1)求m、n的值;
(2)求“C等级”所对应的扇形圆心角的度数;
(3)已知成绩等级为A的4名学生中有1名男生和3名女生,现从中随机挑选2名学生代表学校参加全市比赛,求出恰好选中一男生和一女生的概率
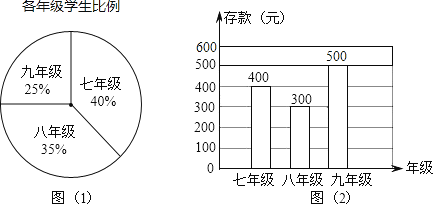
【题目】“倡导全民阅读”“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.某中学在全校学生中随机抽取了部分学生对2018年度阅读情况进行问卷调查,并将收集的数据统计如表
数量/本 | 15 | 11 | 8 | 4 | 3 | 2 |
人数 | 80 | 60 | 50 | 100 | 40 | 70 |
根据表中的信息判断,下列结论错误的是( )
A. 该校参与调查的学生人数为400人
B. 该校学生2018年度阅读书数量的中位数为4本
C. 该校学生2018年度阅读书数量的众数为4本
D. 该校学生2018年平均每人阅读8本书