题目内容
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
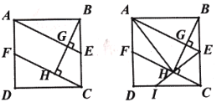
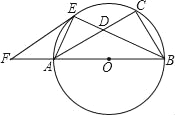
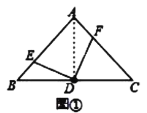
(1)如图①,若点![]() 分别为
分别为![]() 上的点,且
上的点,且![]() ,试探究
,试探究![]() 和
和![]() 的数量关系;并说明四边形
的数量关系;并说明四边形![]() 的面积是定值吗?若是,请求出;若不是,请说明理由.
的面积是定值吗?若是,请求出;若不是,请说明理由.
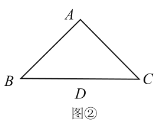
(2)若点![]() 分别为
分别为![]() 延长线上的点,且
延长线上的点,且![]() ,那么
,那么![]() 吗?请利用图②说明理由.
吗?请利用图②说明理由.

【答案】(1)![]() ,四边形
,四边形![]() 的面积是定值,为4;(2)
的面积是定值,为4;(2)![]() ,证明见解析
,证明见解析
【解析】
(1)连接AD,根据等腰直角三角形的性质得到![]() ,
,![]()
![]() ,根据同角的余角相等得到
,根据同角的余角相等得到![]() ,然后利用ASA定理证得
,然后利用ASA定理证得![]() ,从而求得BE与AF的数量关系,然后结合全等三角形的性质求得四边形面积为定值;
,从而求得BE与AF的数量关系,然后结合全等三角形的性质求得四边形面积为定值;
(2)连接AD,根据等角的补角相等,同角的余角相等求得![]() ,
,![]() ,然后理由ASA定理证得
,然后理由ASA定理证得![]() ,从而是问题得解.
,从而是问题得解.
解:(1)如图①所示,连接![]() .
.
![]() ,
,![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.
![]() 点
点![]() 为
为![]() 的中点,
的中点,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,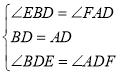 ,
,
![]() ,
,
![]() ;
;
![]()
![]() 四边形
四边形![]() 的面积是定值,总为4.
的面积是定值,总为4.
(2)![]() ,证明如下:连接
,证明如下:连接![]() 如图②所示.
如图②所示.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
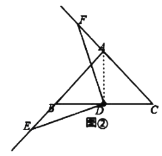
中,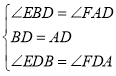 ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目
【题目】某校为了解八年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() .
.![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图中相关数据回答下列问题:
,请结合图中相关数据回答下列问题:
发言次数 | |
|
|
|
|
|
|
|
|
|
|
|
|
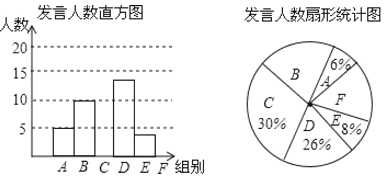
(1)求出样本容量,并补全直方图;
(2)该年级共有学生1500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知![]() 组发言的学生中恰有1位男生,
组发言的学生中恰有1位男生,![]() 组发言的学生中有2位女生.现从
组发言的学生中有2位女生.现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率
组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率