题目内容
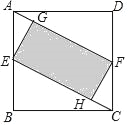
【题目】如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=3![]() x2 B. y=4
x2 B. y=4![]() x2 C. y=8x2 D. y=9x2
x2 C. y=8x2 D. y=9x2
【答案】C
【解析】
设正方形的边长为2a,易证四边形AFCE是平行四边形,所以四边形EHFG是矩形,由∠AEG=∠BCE得到等式,从而可用x表示出EG,接着用x表示EH,从而可求出y与x之间的关系式.
解:设正方形的边长为2a,
∴BC=2a,BE=a,
∵E、F分别是AB、CD的中点,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∵EG⊥AF,FH⊥CE,
∴四边形EHFG是矩形,
∵∠AEG+∠BEC=∠BCE+∠BEC=90°,
∴∠AEG=∠BCE,
∴tan∠AEG=tan∠BCE,
∴![]() ,
,
∴EG=2x,
∴由勾股定理可知:AE=![]() x,
x,
∴AB=BC=![]() x,
x,
∴CE=5x,
易证:△AEG≌△CFH,
∴AG=CH,
∴EH=EC-CH=4x,
∴y=EGEC=8x2,
故选C.

练习册系列答案
相关题目