题目内容
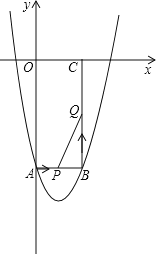
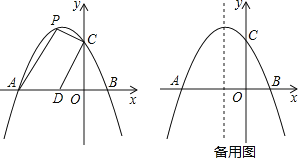
【题目】如图,抛物线y=ax2+bx+2交x轴于点A(-3,0)和点B(1,0),交y轴于点C.
(1)求这个抛物线的函数表达式.
(2)点D的坐标为(-1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.
(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x2-
x2-![]() x+2;(2)S的最大值为
x+2;(2)S的最大值为![]() ;(3)存在,点N的坐标为:(
;(3)存在,点N的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)抛物线的表达式为:y=a(x+3)(x-1)=a(x2+2x-3)=ax2+2ax-3a,即-3a=2,即可求解;
(2)S四边形ADCP=S△APO+S△CPO-S△ODC,即可求解;
(3)分点N在x轴上方、点N在x轴下方两种情况,分别求解.
解:(1)抛物线的表达式为:y=a(x+3)(x-1)=a(x2+2x-3)=ax2+2ax-3a,
即-3a=2,解得:a=-![]() ,
,
故抛物线的表达式为:y=-![]() x2-
x2-![]() x+2,
x+2,
则点C(0,2),函数的对称轴为:x=1;
(2)连接OP,设点P(x,-![]() x2-
x2-![]() x+2),
x+2),
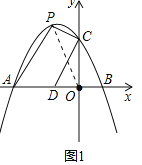
则S=S四边形ADCP=S△APO+S△CPO-S△ODC=![]() ×AO×yP+
×AO×yP+![]() ×OC×|xP|-
×OC×|xP|-![]() ×CO×OD
×CO×OD
=![]() (-
(-![]() x2-
x2-![]() x+2)
x+2)![]() ×2×(-x)-
×2×(-x)-![]() =-x2-3x+2,
=-x2-3x+2,
∵-1<0,故S有最大值,当x=-![]() 时,S的最大值为
时,S的最大值为![]() ;
;
(3)存在,理由:
△MNO为等腰直角三角形,且∠MNO为直角时,点N的位置如下图所示:
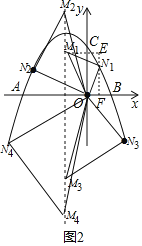
①当点N在x轴上方时,点N的位置为N1、N2,
N1的情况(△M1N1O):
设点N1的坐标为(x,-![]() x2-
x2-![]() x+2),则M1E=x+1,
x+2),则M1E=x+1,
过点N1作x轴的垂线交x轴于点F,过点M1作x轴的平行线交N1F于点E,
∵∠FN1O+∠M1N1E=90°,∠M1N1E+∠EM1N1=90°,∴∠EM1N1=∠FN1O,
∠M1N1E=∠N1OF=90°,ON1=M1N1,
∴△M1N1E≌△N1OF(AAS),∴M1E=N1F,
即:x+1=-![]() x2-
x2-![]() x+2,解得:x=
x+2,解得:x=![]() (舍去负值),
(舍去负值),
则点N1(![]() ,
,![]() );
);
N2的情况(△M2N2O):
同理可得:点N2(![]() ,
,![]() );
);
②当点N在x轴下方时,点N的位置为N3、N4,
同理可得:点N3、N4的坐标分别为:(![]() ,
,![]() )、(
)、(![]() ,
,![]() );
);
综上,点N的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 备战中考寒假系列答案
备战中考寒假系列答案