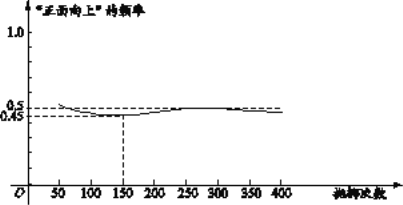
题目内容
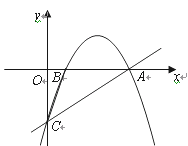
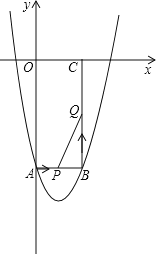
【题目】如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
【答案】(1)![]() (2)①S=(t-3)2+9(0<t<6)②点R坐标为(3,﹣18)
(2)①S=(t-3)2+9(0<t<6)②点R坐标为(3,﹣18)
【解析】解:(1)设抛物线的解析式为y=ax2+bx+c,
由题意知点A(0,﹣12),
所以c=﹣12,
又18a+c=0,
![]() ,
,
∵AB∥OC,且AB=6,
∴抛物线的对称轴是![]() ,
,
∴b=﹣4,
所以抛物线的解析式为![]() ;
;
(2)①![]() ,(0<t<6)
,(0<t<6)
②当t=3时,S取最大值为9.
这时点P的坐标(3,﹣12),
点Q坐标(6,﹣6)
若以P、B、Q、R为顶点的四边形是平行四边形,有如下三种情况:
(Ⅰ)当点R在BQ的左边,且在PB下方时,点R的坐标(3,﹣18),将(3,﹣18)代入抛物线的解析式中,满足解析式,所以存在,点R的坐标就是(3,﹣18),
(Ⅱ)当点R在BQ的左边,且在PB上方时,点R的坐标(3,﹣6),将(3,﹣6)代入抛物线的解析式中,不满足解析式,所以点R不满足条件.
(Ⅲ)当点R在BQ的右边,且在PB上方时,点R的坐标(9,﹣6),将(9,﹣6)代入抛物线的解析式中,不满足解析式,所以点R不满足条件.
综上所述,点R坐标为(3,﹣18).

 阅读快车系列答案
阅读快车系列答案