题目内容
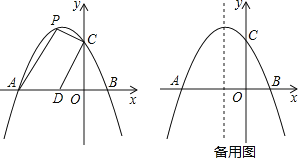
【题目】如图,在平面直角坐标系xoy中,点A的坐标为(0,1),取一点B(b,0),连接AB,作线段AB的垂直平分线![]() ,过点B作X轴的垂线
,过点B作X轴的垂线![]() ,记
,记![]() ,
,![]() 的交点为P。
的交点为P。
(1)当b=3时,在图1中补全图形(尺规作图,不写作法,保留作图痕迹)。
(2)小慧多次取不同数值b,得出相应的点P,并把这些点用平滑的曲线连接起来,发现:这些点P竟然在一条曲线L上。
①设点P的坐标为(x,y),试求y与x之间的关系式,并指出曲线L是哪种曲线。
②设点P到x轴,y轴的距离分别为![]() ,
,![]() ,求
,求![]() +
+![]() 的范围。当
的范围。当![]() +
+![]() =8时,求点P的坐标。
=8时,求点P的坐标。
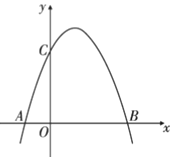
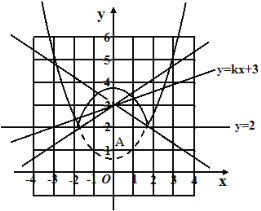
③将曲线在直线y=2下方的部分沿直线y=2向上翻折,得到一条“W”形状的新曲线,若直线y=kx+3与这条“W”形状的新曲线有4个交点,直接写出k的取值范围。
【答案】(1)答案见解析 (2)①![]() ,抛物线 ②(3,5)或(-3,5) ③-
,抛物线 ②(3,5)或(-3,5) ③-![]() <k<
<k<![]()
【解析】
(1)利用尺规作出线段AB的垂直平分线,过点B作出x轴的垂线即可;
(2)①分x>0或x<0两种情形利用勾股定理求出x与y的关系即可解决问题;
②由题意得![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
③求出直线y=2与抛物线![]() y=的两个交点为(-
y=的两个交点为(-![]() ,2)和(
,2)和(![]() ,2),利用这两个特殊点,求出k的值即可解决问题.
,2),利用这两个特殊点,求出k的值即可解决问题.
(1)
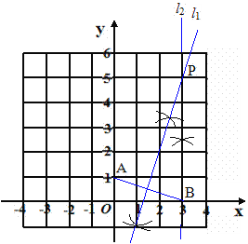
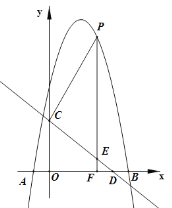
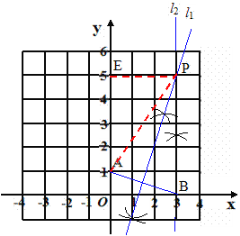
(2)①当x>0时,如图,连接AP,过点P作PE⊥y轴于点E,
∵l1垂直平分AB
∴PA=PB=y.在Rt△APE中,EP=OB=x,AE=OE-OA=y-1,
由勾股定理得:![]() ,整理得:
,整理得:![]() ;
;
当x≤0时,点P(x,y)同样满足![]() ,
,
∴曲线L就是二次函数![]() 的图像.即曲线L是一条抛物线.
的图像.即曲线L是一条抛物线.
②由题意可知,![]() ,d2=|x|
,d2=|x|
∴![]()
当x=0时,d1+d2有最小值![]() ,
,
∴d1+d2的范围是d1+d2≥![]() .
.
当d1+d2=8时,则![]()
(Ⅰ)当x≥0时,原方程化为![]() .解得x1=3,x2= -5(舍去).
.解得x1=3,x2= -5(舍去).
(Ⅱ)当x<0时,原方程化为![]() .解得x1=-3,x2= 5(舍去).
.解得x1=-3,x2= 5(舍去).
将x=±3代入![]() ,得y=5,
,得y=5,
∴点P的坐标为(3,5)或(-3,5);
③k的取值范围是:-![]() <k<
<k<![]() .
.
解答过程如下(过程不需写):把y=2代入![]() ,得x1=-
,得x1=-![]() ,x2=
,x2=![]() .
.
∴直线y=2与抛物线![]() 两个交点的坐标为(-
两个交点的坐标为(-![]() ,2)和(
,2)和(![]() ,2).
,2).
当直线y=kx+3过点(-![]() ,2)时,可求得k=
,2)时,可求得k=![]() ;
;
当直线y=kx+3过点(![]() ,2)时,可求得k=-
,2)时,可求得k=-![]() .
.
故当直线y=kx+3与这条“W”形状的新曲线有4个交点时,k的取值范围是:-![]() <k<
<k<![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
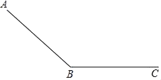
A.270B.280C.375D.450