Question

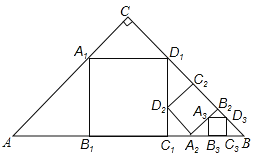
【题目】如图，△ABC，∠C=90°，AC=BC=a，在△ABC中截出一个正方形A1B1C1D1，使点A1，D1分别在AC，BC边上，边B1C1在AB边上；在△BC1D1在截出第二个正方形A2B2C2D2，使点A2，D2分别在BC1，D1C1边上，边B2C2在BD1边上；…，依此方法作下去，则第n个正方形的边长为 ．

Answer 1

【答案】．

【解析】

设正方形A1B1C1D1的边长为x，

∵△CA1D1和△AA1B1都是等腰直角三角形，

∴A1C=，AA1=，

∴，

解得，即第1个正方形的边长为，

设正方形A2B2C2D2的边长为y，

∵△C2D1D2和△C1A2D2都是等腰直角三角形，

∴C1D2=，D1D2=，

∴，

解得y=，

即第2个正方形的边长为，．．．．．．，

同理可得第3个正方形的边长为，

∴第n个正方形的边长为．

故答案为：．