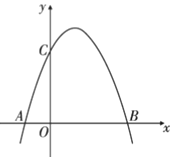
ЬтФПФкШн
ЁОЬтФПЁПЖдгкФГвЛКЏЪ§ИјГіШчЯТЖЈвхЃКЖдгкШЮвтЪЕЪ§![]() ЃЌЕБздБфСП
ЃЌЕБздБфСП![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() Йигк
Йигк![]() ЕФКЏЪ§ЭМЯѓЮЊ
ЕФКЏЪ§ЭМЯѓЮЊ![]() ЃЌНЋ
ЃЌНЋ![]() бижБЯп
бижБЯп![]() ЗелКѓЕУЕНЕФКЏЪ§ЭМЯѓЮЊ
ЗелКѓЕУЕНЕФКЏЪ§ЭМЯѓЮЊ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФЭМЯѓгЩ
ЕФЭМЯѓгЩ![]() КЭ
КЭ![]() СНВПЗжЙВЭЌзщГЩЃЌдђКЏЪ§
СНВПЗжЙВЭЌзщГЩЃЌдђКЏЪ§![]() ЮЊдКЏЪ§ЕФЁАЖделКЏЪ§ЁБЃЌШчКЏЪ§
ЮЊдКЏЪ§ЕФЁАЖделКЏЪ§ЁБЃЌШчКЏЪ§![]() (
(![]() )ЕФЖделКЏЪ§ЮЊ
)ЕФЖделКЏЪ§ЮЊ![]() .
.
(1)ЧѓКЏЪ§![]() (
(![]() )ЕФЖделКЏЪ§ЃЛ
)ЕФЖделКЏЪ§ЃЛ
(2)ШєЕу![]() дкКЏЪ§
дкКЏЪ§![]() (
(![]() )ЕФЖделКЏЪ§ЕФЭМЯѓЩЯЃЌЧѓ
)ЕФЖделКЏЪ§ЕФЭМЯѓЩЯЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(3)ЕБКЏЪ§![]() (
(![]() )ЕФЖделКЏЪ§гы
)ЕФЖделКЏЪ§гы![]() жсгаВЛЭЌЕФНЛЕуИіЪ§ЪБЃЌжБНгаДГі
жсгаВЛЭЌЕФНЛЕуИіЪ§ЪБЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
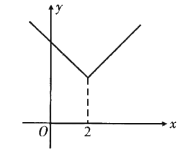
ЁОД№АИЁП(1)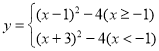 ЃЛ(2)
ЃЛ(2)![]() Лђ-6ЃЛ(3)n<-1ЪБЃЌгыxжсга4ИіНЛЕуЃЌn=-1ЪБЃЌгыxжсга3ИіНЛЕуЃЛ
Лђ-6ЃЛ(3)n<-1ЪБЃЌгыxжсга4ИіНЛЕуЃЌn=-1ЪБЃЌгыxжсга3ИіНЛЕуЃЛ![]() гыxжсга2ИіНЛЕуЃЛn=3ЪБЃЌгыxжсга3ИіНЛЕуЃЛn>3ЪБЃЌгыxжсЮоНЛЕу.
гыxжсга2ИіНЛЕуЃЛn=3ЪБЃЌгыxжсга3ИіНЛЕуЃЛn>3ЪБЃЌгыxжсЮоНЛЕу.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЖЈвхЕУГіЖделКѓКЏЪ§ЕФЖЅЕузјБъЮЊ![]() ЃЌИУКЏЪ§БэДяЪНЮЊЃК
ЃЌИУКЏЪ§БэДяЪНЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНЋЕу![]() ДњШы
ДњШы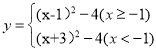 ЧѓНтГіmЕФжЕМДПЩЃЛ
ЧѓНтГіmЕФжЕМДПЩЃЛ
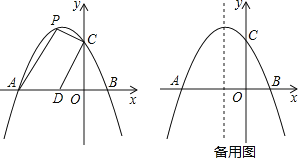
ЃЈ3ЃЉ)ЗжЕБ![]() ЪБЁЂЕБ
ЪБЁЂЕБ![]() ЪБЁЂ ЕБ
ЪБЁЂ ЕБ![]() ЪБЁЂЕБ
ЪБЁЂЕБ![]() ЪБЁЂЕБ
ЪБЁЂЕБ![]() ЪБЃЌЛГіОпЬхЕФКЏЪ§ЭМЯёНјааЙлВьгыxжсЕФНЛЕуИіЪ§МДПЩ
ЪБЃЌЛГіОпЬхЕФКЏЪ§ЭМЯёНјааЙлВьгыxжсЕФНЛЕуИіЪ§МДПЩ
(1)Сю![]() ЃЌдђ
ЃЌдђ![]() Лђ3ЃЌШчЭМ1ЃКМДЕу
Лђ3ЃЌШчЭМ1ЃКМДЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌдђЖделКѓКЏЪ§ЕФЖЅЕузјБъЮЊ
ЃЌдђЖделКѓКЏЪ§ЕФЖЅЕузјБъЮЊ![]() ЃЌИУКЏЪ§БэДяЪНЮЊЃК
ЃЌИУКЏЪ§БэДяЪНЮЊЃК![]() ЃЌ
ЃЌ
МДЖделКЏЪ§ЮЊ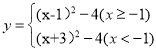 .
.
(2)НЋЕу![]() ДњШы
ДњШы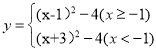
НтЕУЃК![]() Лђ-6(ВЛКЯЬтвтЕФжЕвбЩсШЅ)
Лђ-6(ВЛКЯЬтвтЕФжЕвбЩсШЅ)
МД![]() Лђ-6ЃЛ
Лђ-6ЃЛ
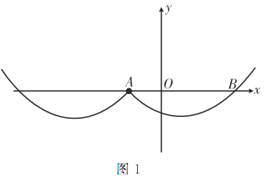
(3)ЂйЕБ![]() ЪБЃЌШчЭМ2ЃК
ЪБЃЌШчЭМ2ЃК
ДЫЪБ![]() дкЕу
дкЕу![]() ЕФзѓВрЃЌДгЭМжаПЩвдПДГіЃККЏЪ§гы
ЕФзѓВрЃЌДгЭМжаПЩвдПДГіЃККЏЪ§гы![]() жсга4ИіНЛЕу
жсга4ИіНЛЕу![]() ЃЛ
ЃЛ
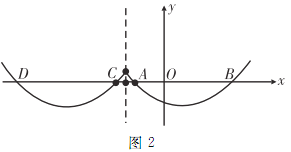
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Й§Еу
Й§Еу![]() ЃЌДгЭМ1ПЩвдПДГіЃККЏЪ§гы
ЃЌДгЭМ1ПЩвдПДГіЃККЏЪ§гы![]() жсга3ИіНЛЕуЃЛ
жсга3ИіНЛЕуЃЛ
ЂлЭЌРэЃКЕБ![]() ЪБЃЌКЏЪ§гы
ЪБЃЌКЏЪ§гы![]() жсга2ИіНЛЕуЃЛ
жсга2ИіНЛЕуЃЛ
ЂмЭЌРэЃКЕБ![]() ЪБЃЌКЏЪ§гы
ЪБЃЌКЏЪ§гы![]() жсга3ИіНЛЕуЃЛ
жсга3ИіНЛЕуЃЛ
ЂнЭЌРэЃКЕБ![]() ЪБЃЌЮоНЛЕу.
ЪБЃЌЮоНЛЕу.

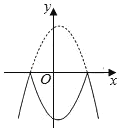
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=x2Љ2xЉ1ЃЎ
x | Ё | Љ1 | 0 | 1 | 2 | 3 | Ё |
y | Ё | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | Ё |
ЃЈ1ЃЉЧыдкБэФкЕФПеИёжаЬюШыЪЪЕБЕФЪ§ЃЛ
ЃЈ2ЃЉИљОнСаБэЃЌЧыдкЫљИјЕФЦНУцжБНЧзјБъЯЕжаЛГіy=x2Љ2xЉ1ЕФЭМЯѓЃЛ
ЃЈ3ЃЉЕБxдкЪВУДЗЖЮЇФкЪБЃЌyЫцxдіДѓЖјМѕаЁЃЛ
ЁОЬтФПЁПвЛИіЛЌЕРгЩЛЌЦТЃЈABЖЮЃЉКЭЛКГхДјЃЈBCЖЮЃЉзщГЩЃЌШчЭМЫљЪОЃЌЛЌбЉепдкЛЌЦТЩЯЛЌааЕФОрРыyЃЈЕЅЮЛЃКmЃЉКЭЛЌааЪБМфt1ЃЈЕЅЮЛЃКsЃЉТњзуЖўДЮКЏЪ§ЙиЯЕЃЌВЂВтЕУЯрЙиЪ§ОнЃК
ЛЌааЪБМфt1/s | 0 | 1 | 2 | 3 | 4 |
ЛЌааОрРыy1/s | 0 | 4.5 | 14 | 28.5 | 48 |
ЛЌбЉепдкЛКГхДјЩЯЛЌааЕФОрРыy2ЃЈЕЅЮЛЃКmЃЉКЭдкЛКГхДјЩЯЛЌааЪБМфt2ЃЈЕЅЮЛЃКsЃЉТњзуЃКy2ЃН52t2Љ2t22ЃЌЛЌбЉепДгAГіЗЂдкЛКГхДјBCЩЯЭЃжЙЃЌвЛЙВгУСЫ23sЃЌдђЛЌЦТABЕФГЄЖШЃЈЁЁЁЁЃЉУз
A.270B.280C.375D.450