题目内容
如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过O点作MN∥BC,分别交AB,AC于M,N.
(1)图中等腰三角形共有______个(已知的△ABC除外)
(2)求证:△BMO是等腰三角形;
(3)求证:MN=2BM.
(4)△ABC中,AB=AC,M,N分别是AB,AC上的点,且AM=AN,O为MN的中点,则BO,CO分别是∠ABC与∠ACB的角平分线,这个结论对吗?请直接回答.
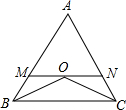
(1)图中等腰三角形共有______个(已知的△ABC除外)
(2)求证:△BMO是等腰三角形;
(3)求证:MN=2BM.
(4)△ABC中,AB=AC,M,N分别是AB,AC上的点,且AM=AN,O为MN的中点,则BO,CO分别是∠ABC与∠ACB的角平分线,这个结论对吗?请直接回答.

(1)△BOM,△CON,△BOC,△AMN,△ABC均为等腰三角形,
所以,除△ABC外还有4个;
(2)证明:∵BO是∠ABC的平分线,
∴∠MBO=∠CBO,
∵MN∥BC,
∴∠CBO=∠MOB,
∴∠MBO=∠MOB,
∴△BMO是等腰三角形;
(3)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,
∴AM=AN,
∴AB-AM=AC-AN,
即BM=CN,
根据(2)△BMO是等腰三角形,
∴BM=OM,
同理可得CN=ON,
∴MN=OM+ON=BM+CN=2BM;
(4)结论不正确;
∵O为MN中点,
∴OM=ON,
又∵MN∥BC,
∴∠BMO=∠CNO,BM=CN,
在△BOM和△CON中,
,
∴△BOM≌△CON(SAS),
∴∠OBM=∠OCN,
又∵AB=AC,
∴∠ABC=∠ACB,
∴∠OBC=∠OCB,
但不能肯定∠OBM=∠OBC,
即不能确定其为角平分线.
∴此问结论不正确.
所以,除△ABC外还有4个;
(2)证明:∵BO是∠ABC的平分线,
∴∠MBO=∠CBO,
∵MN∥BC,
∴∠CBO=∠MOB,
∴∠MBO=∠MOB,
∴△BMO是等腰三角形;
(3)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,
∴AM=AN,
∴AB-AM=AC-AN,
即BM=CN,
根据(2)△BMO是等腰三角形,
∴BM=OM,
同理可得CN=ON,
∴MN=OM+ON=BM+CN=2BM;
(4)结论不正确;
∵O为MN中点,
∴OM=ON,
又∵MN∥BC,
∴∠BMO=∠CNO,BM=CN,
在△BOM和△CON中,
|
∴△BOM≌△CON(SAS),
∴∠OBM=∠OCN,
又∵AB=AC,
∴∠ABC=∠ACB,
∴∠OBC=∠OCB,
但不能肯定∠OBM=∠OBC,
即不能确定其为角平分线.
∴此问结论不正确.

练习册系列答案
相关题目