��Ŀ����
����Ŀ��(��������9��)
����ͬѧ��һ�ο����У���ӲֽƬ��������ֱ�������Σ���ͼ��������ͼ���У�![]() ��
��![]() ��
��![]() ��ͼ���У�
��ͼ���У�![]() ��
��![]() ��
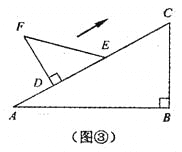
��![]() ��ͼ��������ͬѧ������һ��ʵ�飺����
��ͼ��������ͬѧ������һ��ʵ�飺����![]() ��ֱ�DZ�
��ֱ�DZ�![]() ��
��![]() ���
��б��![]() �غ���һ�𣬲���
�غ���һ�𣬲���![]() ��
��![]() �����ƶ������ƶ������У�
�����ƶ������ƶ������У�![]() ��
��![]() ����ʼ����
����ʼ����![]() ����(�ƶ���ʼʱ��
����(�ƶ���ʼʱ��![]() ���
���![]() �غ�)��
�غ�)��
(1)��![]() ��
��![]() �����ƶ��Ĺ����У�����ͬѧ���֣�
�����ƶ��Ĺ����У�����ͬѧ���֣�![]() ��
��![]() �����ľ����� �� ��
�����ľ����� �� ��
(���������������������������)
(2)����ͬѧ������һ�����о����������������⣺
����������![]() �ƶ���ʲôλ�ã���
�ƶ���ʲôλ�ã���![]() �ij�Ϊ����ʱ��
�ij�Ϊ����ʱ��![]() ��
��![]() ��������
��������![]() ƽ��?
ƽ��?
����������![]() �ƶ���ʲôλ�ã���
�ƶ���ʲôλ�ã���![]() �ij�Ϊ����ʱ�����߶�
�ij�Ϊ����ʱ�����߶�![]() ��
��![]() ��
��![]() �ij���Ϊ���߳�����������ֱ��������?
�ij���Ϊ���߳�����������ֱ��������?
����������![]() ���ƶ������У��Ƿ����ij��λ�ã�ʹ��
���ƶ������У��Ƿ����ij��λ�ã�ʹ��![]() ?������ڣ�
?������ڣ�
���![]() �ij��ȣ���������ڣ���˵�����ɣ�
�ij��ȣ���������ڣ���˵�����ɣ�
����ֱ����������������Ľ����̣�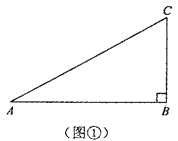
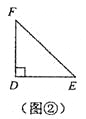
���𰸡���1����С
��2��
��![]() cmʱ��
cmʱ��![]()
����![]() ʱ�����߶�
ʱ�����߶�![]() ��
��![]() ��
��![]() �ij���Ϊ���߳�����������ֱ��������
�ij���Ϊ���߳�����������ֱ��������
��������������λ�ã�ʹ��![]()
��������
��1����С
��2�����������⣺��![]() ��
��![]() ��
��![]() ��
��
��![]() .
.
��![]() ,
,![]() ,
,
��![]() .
.
����![]() ����
����![]() .
.
��![]() ,��
,��![]() ��DC=4.
�У�DC=4.
��![]() =12-4.
=12-4.
��![]() cmʱ��
cmʱ��![]()
���������⣺�赱![]() ��
��
��![]() ��
�У�![]() .
.
��������![]() Ϊб��ʱ����
Ϊб��ʱ����![]() �ã�
�ã�![]() ,
,![]() .
.
(��)��![]() Ϊб��ʱ����
Ϊб��ʱ����![]() �ã�
�ã�![]() ,
,![]() �����������⣬��ȥ��.
�����������⣬��ȥ��.
(��)��![]() Ϊб��ʱ����
Ϊб��ʱ����![]() �ã�
�ã�![]() ,
,![]() ,
,
![]() =144-248<0,
=144-248<0,
��������.
����(��)��(��)��(��)�ã�
��![]() ʱ�����߶�
ʱ�����߶�![]() ��
��![]() ��
��![]() �ij���Ϊ���߳�����������ֱ��������.
�ij���Ϊ���߳�����������ֱ��������.
������������������λ�ã�ʹ��![]() .
.
����![]() ����
����![]() ,��
,��![]() .��
.��![]() ��ƽ���ߣ���
��ƽ���ߣ���![]() ��
��![]() ,
,
��![]() ,
,
��![]() .
.
��![]() ,
,![]() .
.
��![]() .
.
��������������λ�ã�ʹ��![]() .
.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�