题目内容
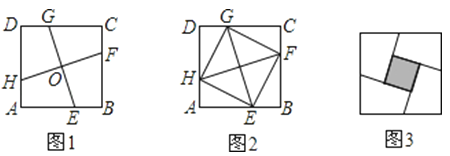
【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x-2经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s=![]() ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.

【答案】(1)y="-1/4" x2+3/2 x-2(2)1(3)当t="2" /3 或t="10/" 7 时,以P、B、D为顶点的三角形与△ABC相似,证明见解析
【解析】试题分析:(1)首先根据直线AC的解析式确定点A、C的坐标,已知AB的长,进一步能得到点B的坐标;然后由待定系数法确定抛物线的解析式;(2)根据所给的s表达式,要解答该题就必须知道ED、OP的长;BP、CE长由计算可知,那么由OP=OB﹣BP求得OP长,由∠CED的三角函数值可得到ED的长,再代入s的表达式中可得到关于s、t的函数关系式,结合函数的性质即可得到s的最小值;(3)首先求出BP、BD的长,若以P、B、D为顶点的三角形与△ABC相似,已知的条件是公共角∠OBC,那么必须满足的条件是夹公共角的两组对应边成比例,分两种情况讨论即可.
试题解析:(1)由直线:y=x﹣2知:A(2,0)、C(0,﹣2);∵AB=2,∴OB=OA+AB=4,即B(4,0).设抛物线的解析式为:y=a(x﹣2)(x﹣4),代入C(0,﹣2),得:a(0﹣2)(0﹣4)=﹣2,解得 a=﹣![]() ,∴抛物线的解析式:y=﹣
,∴抛物线的解析式:y=﹣![]() (x﹣2)(x﹣4)=﹣
(x﹣2)(x﹣4)=﹣![]() x2+
x2+![]() x﹣2;(2)在Rt△OBC中,OB=4,OC=2,则tan∠OCB=2;∵CE=t,∴DE=2t,而OP=OB﹣BP=4﹣2t;
x﹣2;(2)在Rt△OBC中,OB=4,OC=2,则tan∠OCB=2;∵CE=t,∴DE=2t,而OP=OB﹣BP=4﹣2t;
∴s=![]() =
=![]() =
= (0<t<2),∴当t=1时,s有最小值,且最小值为1.
(0<t<2),∴当t=1时,s有最小值,且最小值为1.
(3)在Rt△OBC中,OB=4,OC=2,则BC=2![]() ;在Rt△CED中,CE=t,ED=2t,则CD=
;在Rt△CED中,CE=t,ED=2t,则CD=![]() t;
t;
∴BD=BC﹣CD=2![]() ﹣
﹣![]() t;若以P、B、D为顶点的三角形与△ABC相似,已知∠OBC=∠PBD,则有两种情况:①
t;若以P、B、D为顶点的三角形与△ABC相似,已知∠OBC=∠PBD,则有两种情况:①![]()
![]() =
=![]() ,解得 t=
,解得 t=![]() ;②
;②![]()
![]() =
=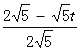 ,解得 t=
,解得 t=![]() ;综上所述,当t=
;综上所述,当t=![]() 或
或![]() 时,以P、B、D为顶点的三角形与△ABC相似.
时,以P、B、D为顶点的三角形与△ABC相似.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案