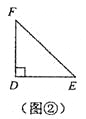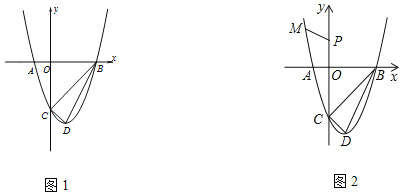��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���P������Ϊ��x1��y1������Q������Ϊ��x2��y2������x1��x2��y1��y2����P��QΪij�����ε��������㣬�Ҹþ��εı߾���ij�������ᴹֱ����Ƹþ���Ϊ��P��Q�ġ���ؾ��Ρ�����ͼ��Ϊ��P��Q�ġ���ؾ��Ρ���ʾ��ͼ��
��֪��A������Ϊ��1��0����
��1������B������Ϊ��3��1�������A��B�ġ���ؾ��Ρ��������
��2����C��ֱ��x��3�ϣ�����A��C�ġ���ؾ��Ρ�Ϊ�����Σ���ֱ��AC�ı���ʽ��
��3������D������Ϊ��4��2������ֱ��y��2x+bƽ�ƣ��������A��D�ġ���ؾ��Ρ�û�й�����ʱ�����b��ȡֵ��Χ��
���𰸡���1��2����2��![]() ��
��![]() ����3��
����3��![]() ��
��![]()
��������
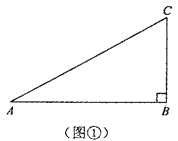
��1������ؾ��εĶ����֪��Ҫ��A��B����ؾ����������AB��Ϊ�Խ��ߣ�����A��B��������꼴������þ��εĵ���ߵij��ȣ�����������þ��ε������
��2���ɶ����֪��AC��Ϊ�����εĶԽ��ߣ�����AC��x��ļнDZ�Ϊ45����ֱ��AC�Ľ���ʽΪ��y=kx+b���ɴ˿�֪k=��1���٣�1��0������y=kx+b���������b��ֵ��
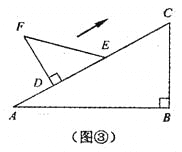
��3���ֱ�ѵ�A��D����������y=2x+b��2�����b����ֵ���ɣ�
��1����A��1��0����B��3��1��
�ɶ����֪����A��B������ؾ������ĵ���߷ֱ�Ϊ2��1��
���A��B������ؾ����������Ϊ2��1=2��
��2���ɶ����֪��AC�ǵ�A��C������ؾ������ĶԽ��ߣ�
�֡ߵ�A��C������ؾ�����Ϊ������
��ֱ��AC��x��ļн�Ϊ45����
��ֱ��AC�Ľ���Ϊ��y=x+m��y=-x+n
�ѣ�1��0���ֱ�y=x+m��
��m=-1��
��ֱ��AC�Ľ���Ϊ��y=x-1��
�ѣ�1��0������y=-x+n��
��n=1��
��y=-x+1��
��������������A��C������ؾ�����Ϊ�����Σ�ֱ��AC�ı���ʽΪy=x-1��y=-x+1��
��3����A��1��0����D��4��2���ֱ����y=2x+b��2��
�ó�b=0����b=-8��
��b��0��b��-8

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
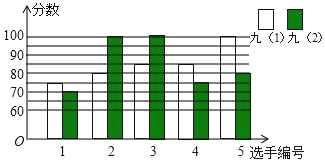
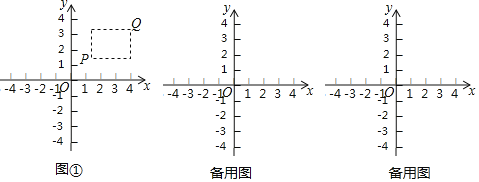
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�����Ŀ��Ϊѡ������ѡ�ֲμ��������ڰ˽�����Ļ������ڡ��о��䡱����������꼶��1������2������ݳ����ɼ�����ѡ��5��ѡ�ֲμӸ������������ѡ����5��ѡ�ֵĸ����ɼ���ͼ��ʾ
��1������ͼʾ��д�±�
�༶ | ƽ�������֣� | ��λ�����֣� | �������֣� |
�ţ�1�� | 85 | �� �� | 85 |
�ţ�2�� | �� �� | 80 | �� �� |
��2��������ิ���ɼ���ƽ��������λ���������ĸ��༶�ĸ����ɼ��Ϻã�
��3���������ิ���ɼ��ķ����˵���ĸ�������ѡ�ֵijɼ����ȶ���