题目内容
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+3a(a>0)与x轴交于A,B两点(A在B的左侧).
(1)求抛物线的对称轴及点A,B的坐标;
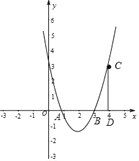
(2)点C(t,3)是抛物线y=ax2﹣4ax+3a(a>0)上一点,(点C在对称轴的右侧),过点C作x轴的垂线,垂足为点D.
①当CD=AD时,求此时抛物线的表达式;
②当CD>AD时,求t的取值范围.
【答案】(1) A(1,0),B(3,0);(2) ①y=x2﹣4x+3;②3<t<4.
【解析】分析:(1)令函数值为0得到ax2-4ax+3a=0,然后解方程可得到A点和B点坐标;利用抛物线的对称轴方程确定抛物线的对称轴;
(2)①利用点C的坐标得到CD=3,OA=t,则AD=t-1,根据题意得到t-1=3,解方程求出t得到C(4,3),然后把C点坐标代入y=ax2-4ax+3a中求出a即可得到抛物线解析式;
②利用CD>AD得到3>t-1,再利用点C在B点的右侧得到t >3,从而可确定t的范围.
详解:(1)当y=0时,ax2﹣4ax+3a=0,即x2﹣4x+3=0,解得x1=1,x2=3,
∴A(1,0),B(3,0),
抛物线的对称轴为直线x=﹣![]() =2;
=2;
(2)①∵CD⊥x轴,
∴CD=3,OD=t,
∴AD=t﹣1,
而CD=AD,
∴t﹣1=3,解得t=4,
∴C(4,3),
把C(4,3)代入y=ax2﹣4ax+3a得16a﹣16a+3a=3,解得a=1,
∴此时抛物线解析式为y=x2﹣4x+3;
②∵CD>AD,
∴3>t﹣1,
∴t<4,
而点C在点B的右侧,
∴t>3,
∴t的范围为3<t<4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目