题目内容
如图,在正方形ABCD中,E为对角线AC上一点,联结EB、ED,延长BE交AD于点F.
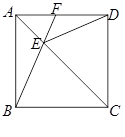
(1)求证:∠BEC =∠DEC ;
(2)当CE=CD时,求证: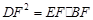 .
.

(1)求证:∠BEC =∠DEC ;
(2)当CE=CD时,求证:
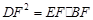 .
.(1)∵四边形ABCD是正方形,∴BC=CD,且∠BCE=∠DCE.
又∵CE是公共边,∴△BEC≌△DEC,
∴∠BEC =∠DEC.
(2)联结BD .
∵CE=CD,∴∠DEC =∠EDC.
∵∠BEC =∠DEC,∠BEC =∠AEF,∴∠EDC=∠AEF.
∵∠AEF+∠FED=∠EDC+∠ECD,
∴∠FED=∠ECD.
∵四边形ABCD是正方形,
∴∠ECD= ∠BCD =45°, ∠ADB=
∠BCD =45°, ∠ADB= ∠ADC= 45°,∴∠ECD=∠ADB.… (1分)
∠ADC= 45°,∴∠ECD=∠ADB.… (1分)
∴∠FED=∠ADB.
又∵∠BFD是公共角,∴△FDE∽△FBD,
∴ ,即
,即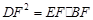
又∵CE是公共边,∴△BEC≌△DEC,
∴∠BEC =∠DEC.
(2)联结BD .
∵CE=CD,∴∠DEC =∠EDC.
∵∠BEC =∠DEC,∠BEC =∠AEF,∴∠EDC=∠AEF.
∵∠AEF+∠FED=∠EDC+∠ECD,
∴∠FED=∠ECD.
∵四边形ABCD是正方形,
∴∠ECD=
 ∠BCD =45°, ∠ADB=
∠BCD =45°, ∠ADB= ∠ADC= 45°,∴∠ECD=∠ADB.… (1分)
∠ADC= 45°,∴∠ECD=∠ADB.… (1分)∴∠FED=∠ADB.
又∵∠BFD是公共角,∴△FDE∽△FBD,
∴
 ,即
,即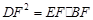
此题主要考核全等三角形的性质和相似三角形的性质

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 ;
;  DO∥AB
DO∥AB CD=AD;
CD=AD; △BDE∽△BCD;
△BDE∽△BCD; 
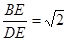

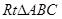 中,
中,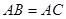 ,
,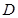 为斜边
为斜边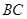 上的动点,若
上的动点,若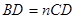 ,
,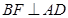 交
交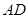 于
于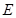 、
、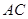 于
于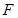 .
.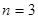 时,则
时,则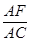 = ;
= ;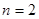 时,求证:
时,求证: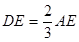
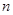 = 时,
= 时,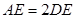 .
.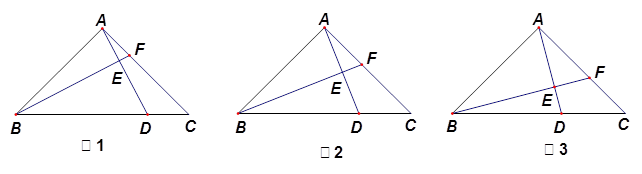
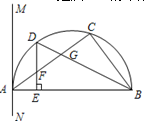
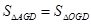 ;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有 ( ▲ )
;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有 ( ▲ )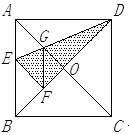
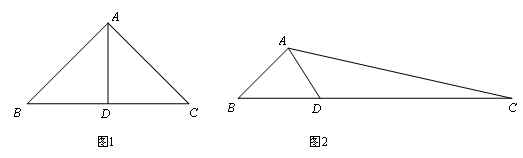
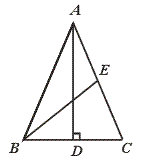
 ,求AD的长及△ACD的面积.
,求AD的长及△ACD的面积. 中,点
中,点 分别在边
分别在边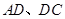 上,
上,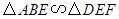
 ,求
,求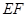 的长
的长