题目内容
(本题10分)
如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
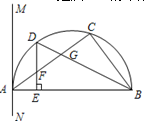
(1)求证:MN是半圆的切线;
(2)求证:FD=FG;
(3)若△DFG的面积为4.5,且DG=3,GC=4,试求△BCG的面积.
如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.

(1)求证:MN是半圆的切线;
(2)求证:FD=FG;
(3)若△DFG的面积为4.5,且DG=3,GC=4,试求△BCG的面积.
(1)证明: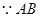 是直径,
是直径,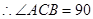 °即
°即
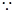 ∠MAC=∠ABC,
∠MAC=∠ABC,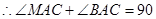 °,即
°,即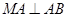
所以MN是半圆的切线;
(2) ∵D是弧AC的中点,∴∠DBC=∠2
∵AB是直径,∴∠CBG+∠CGB=90º
∵DE⊥AB,∴∠FDG+∠2=90º
∵∠DBC=∠2,∴∠FDG=∠CGB=∠FGD
∴FD=F∵∠ADB=90º,DE⊥AB,∴∠3=∠2
∵∠1=∠2,∴∠1=∠3
∴AF=DF=FG
(3)∵∠ADG=∠BCG,∠DGA=∠CGB
∴△ADG∽△BCG
∴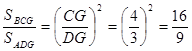
∴S△BCG=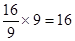
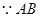 是直径,
是直径,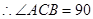 °即
°即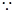 ∠MAC=∠ABC,
∠MAC=∠ABC,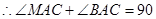 °,即
°,即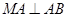
所以MN是半圆的切线;
(2) ∵D是弧AC的中点,∴∠DBC=∠2
∵AB是直径,∴∠CBG+∠CGB=90º
∵DE⊥AB,∴∠FDG+∠2=90º
∵∠DBC=∠2,∴∠FDG=∠CGB=∠FGD
∴FD=F∵∠ADB=90º,DE⊥AB,∴∠3=∠2
∵∠1=∠2,∴∠1=∠3
∴AF=DF=FG
(3)∵∠ADG=∠BCG,∠DGA=∠CGB
∴△ADG∽△BCG
∴
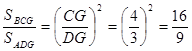
∴S△BCG=
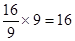
此题考查切线的判定、圆的有关知识、三角形的面积。

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
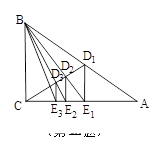
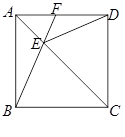
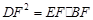 .
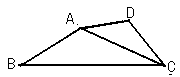
.
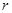 的⊙
的⊙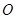 ,对于任意点
,对于任意点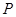 ,在射线
,在射线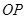 上取一点
上取一点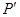 ,使得
,使得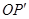 =
= ,这种把点
,这种把点
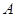 、
、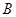 ,它们的反演点分别是
,它们的反演点分别是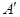 、
、 ,则与∠
,则与∠
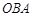
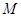 ,请用尺规作图画出点
,请用尺规作图画出点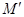 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法).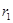 的⊙
的⊙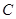 ,作射线
,作射线 交⊙
交⊙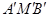 =90°.
=90°.