题目内容
【题目】已知,如图,在平面直角坐标系![]() 中,双曲线
中,双曲线![]() 与直线
与直线![]() 都经过点
都经过点![]() .
.
(1)求![]() 与
与![]() 的值;
的值;
(2)此双曲线又经过点![]() ,点
,点![]() 是
是![]() 轴的负半轴上的一点,且点
轴的负半轴上的一点,且点![]() 到
到![]() 轴的距离是2 ,联结
轴的距离是2 ,联结![]() 、
、![]() 、
、![]() ,
,
①求![]() 的面积;
的面积;
②点![]() 在
在![]() 轴上,
轴上,![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)k=8,m=4;(2)①8;②![]()
【解析】
(1)利用一次函数图象上点的坐标特征可求出m的值,进而可得出点A的坐标,再利用反比例函数图象上点的坐标特征可求出k的值;
(2)①由(1)可得出双曲线的表达式,利用反比例函数图象上点的坐标特征可得出点B的坐标,由点C的位置可得出点C的坐标,由点A,B,C的坐标可得出AB,AC,BC的长,由AB2+BC2=AC2可得出∠ABC=90°,利用三角形的面积公式可求出△ABC的面积;
②设点E的坐标为(0,a),由点A,C的坐标可得出AC2,AE2,CE2的值,分AE=AC,CE=AC,CE=AE三种情况,可得出关于a的一元二次方程(或一元一次方程),解之即可得出结论.
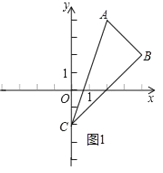
解:(1)∵直线y=2x经过点A(2,m),
∴m=2×2=4,
∴点A的坐标为(2,4).
∵双曲线![]() 经过点A(2,4),
经过点A(2,4),
∴4=![]() ,
,
∴k=8.
(2)①由(1)得:双曲线的表达式为y=![]() .
.
∵双曲线y=![]() 经过点B(n,2),
经过点B(n,2),
∴2=![]() ,
,
∴n=4,
∴点B的坐标为(4,2).
∵点C是y轴的负半轴上的一点,且点C到x轴的距离是2,
∴点C的坐标为(0,2),
∴AB=![]() ,
,
BC=![]() ,
,
AC=![]() .
.
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2,
)2,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴S△ABC=![]() ABBC=
ABBC=![]() ×
×![]() ×
×![]() =8.
=8.
②设点E的坐标为(0,a),
∴AE2=(02)2+(a4)2=a28a+20,CE2=[a(2)]2=a2+4a+4,AC2=40.
分三种情况考虑,如图2所示.
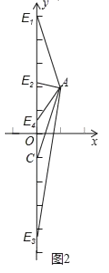
(i)当AE=AC时,a28a+20=40,
解得:a1=2(舍去),a2=10,
∴点E1的坐标为(0,10);
(ii)当CE=AC时,a2+4a+4=40,
解得:a3=2+2![]() ,a4=22
,a4=22![]() ,
,
∴点E2的坐标为(0,2+2![]() ),点E3的坐标为(0,22
),点E3的坐标为(0,22![]() );
);
(iii)当CE=AE时,a2+4a+4=a28a+20,
解得:a=![]() ,
,
∴点E4的坐标为(0,![]() ).
).
综上所述:点E的坐标为(0,10),(0,2+2![]() ),(0,22
),(0,22![]() )或(0,
)或(0,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案