题目内容
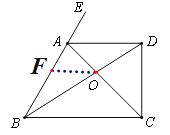
【题目】如图,AC,BD相交于点O,AC平分∠DCB,CD⊥AD,∠ACD=45°,∠BAC=60°.
(1)证明:AD∥BC;
(2)求∠EAD的度数;
(3)求证:∠AOB=∠DAC +∠CBD

【答案】(1)见解析;(2)75°;(3)见解析.
【解析】(1)由AC平分∠DCB,∠ACD=45°,可得∠BCD=90°,从而可证AD∥BC;
(2)由AD∥BC可求∠ACB=∠ACD=45°,然后由三角形内角和可求出∠ABC的度数,再根据两直线平行,同位角相等可求出∠EAD的度数;;
(3)过点O作OF∥AD,则OF∥BC,根据平行线的性质可得∠AOF=∠DAC,∠FOB=∠CBD,然后等量代换可得结论.
⑴ 证明:∵AC平分∠DCB,
∴∠BCD=2∠ACD=2×45°=90°.
∵CD⊥AD,
∴∠ADC=90°,
∴∠BCD+∠ADC=90°+90°=180°,
∴AD∥BC;
⑵ ∵AC平分∠DCB,
∴∠ACB=∠ACD=45°,
∵AD∥BC,
∴∠DAC=∠ACB=45°,
∴∠EAD=180°-∠DAC-∠BAC
=180°-45°-60°
=75°;
⑶ 过点O作OF∥AD,
∵AD∥BC,
∴OF∥BC,
∴∠AOF=∠DAC,∠FOB=∠CBD,
∴∠AOB=∠AOF+∠FOB=∠DAC+∠CBD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目