题目内容
【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
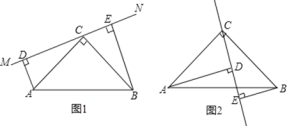
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
【答案】(1)①见解析,②见解析;(2)DE=AD-BE,证明见解析.
【解析】
(1)①先利用同角的余角相等证得∠DAC=∠ECB,再根据AAS即可证得结论;②根据①的结论可得AD=CE,DC=EB,进一步即得结论;
(2)同(1)的证法得出△ADC≌△CEB,根据全等三角形的性质可得AD=CE,DC=BE,进一步即可得出结论.
(1)证明:①∵∠ACD+∠ACB+∠BCE=180°,∠ACB=90°,
∴∠ACD+∠BCE=90°.
∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,

∴△ADC≌△CEB(AAS).
②由①知:△ADC≌△CEB,
∴AD=CE,DC=EB,
∵DE=CE+DC,
∴DE=AD+EB;

(2)DE=AD-BE.
证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠BEC=90°,∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC.
在△ADC和△CEB中,

∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CE-CD=AD-BE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某数学实验小组在探究“关于x的二次三项式ax2+bx+3的性质(a、b为常数)”时,进行了如下活动.
(实验操作)取不同的x的值,计算代数式ax2+bx+3的值.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
ax2+bx+3 | … | 0 | 3 | 4 | … |
(1)根据上表,计算出a、b的值,并补充完整表格.(观察猜想)实验小组组员,观察表格,提出以下猜想.同学甲说:“代数式ax2+bx+3的值随着x的增大而增大”.同学乙说:“不论x取何值,代数式ax2+bx+3的值一定不大于4”.…
(2)请你也提出一个合理的猜想: (验证猜想)我们知道,猜想有可能是正确的,也可能是错误的.
(3)请你分别判断甲、乙两位同学的猜想是否正确,若不正确,请举出反例;若正确,请加以说理.




