Question

【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____

Answer 1

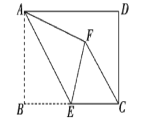
【答案】

【解析】

分析题意,如图所示,连接BF,由翻折变换可知,BF⊥AE,BE=EF,由点E是BC的中点可知BE=3,根据勾股定理即可求得AE；根据三角形的面积公式可求得BH,进而可得到BF的长度;结合题意可知FE=BE=EC,进而可得∠BFC=90°,至此,在Rt△BFC中,利用勾股定理求出CF的长度即可

如图,连接BF.

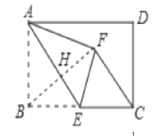
∵△AEF是由△ABE沿AE折叠得到的,

∴BF⊥AE,BE=EF.

∵BC=6,点E为BC的中点,

∴BE=EC=EF=3

根据勾股定理有AE=AB+BE

代入数据求得AE=5

根据三角形的面积公式

得BH=

即可得BF=

由FE=BE=EC,

可得∠BFC=90°

再由勾股定理有BC-BF=CF

代入数据求得CF=

故答案为