题目内容
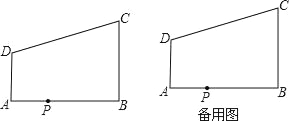
【题目】如图,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,求AP的长.
【答案】AP=![]() 或AP=2或AP=6
或AP=2或AP=6
【解析】试题分析:由AD//BC, ∠B=90°,可证∠PAD=∠PBC=90°, 又由AB=8,AD=3,BC=4,设AP的长为x,则BP长为8-x,然后分别从APD∽△BPC与△APD∽△BCP去分析,利用相似三角形的对应边成比例求解即可求得答案.
试题解析:∵ AB⊥BC,
∴ ∠B=90°,
∵ AD∥BC,
∴ ∠A=180°﹣∠B=90°,
∴ ∠PAD=∠PBC=90°,
AB=8,AD=3,BC=4,
设AP的长为x,则BP长为8﹣x,
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,
解得x=![]() ,
,
若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),
解得x=2或x=6,
所以AP=![]() 或AP=2或AP=6.
或AP=2或AP=6.

练习册系列答案
相关题目