题目内容
【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
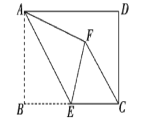
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
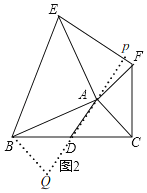
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

【答案】(1)2<AD<7;(2)AC∥BQ,理由见解析;(3)EF=2AD,AD⊥EF,理由见解析
【解析】
(1)先判断出BD=CD,进而得出△QDB≌△ADC(SAS),得出BQ=AC=5,最后用三角形三边关系即可得出结论;
(2)由(1)知,△QDB≌△ADC(SAS),得出∠BQD=∠CAD,即可得出结论;
(3)同(1)的方法得出△BDQ≌△CDA(SAS),则∠DBQ=∠ACD,BQ=AC,进而判断出∠ABQ=∠EAF,进而判断出△ABQ≌△EAF,得出AQ=EF,∠BAQ=∠AEF,即可得出结论.
解:(1)延长AD到Q使得DQ=AD,连接BQ,
∵AD是△ABC的中线,
∴BD=CD,
在△QDB和△ADC中,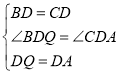 ,
,
∴△QDB≌△ADC(SAS),
∴BQ=AC=5,
在△ABQ中,AB﹣BQ<AQ<AB+BQ,
∴4<AQ<14,
∴2<AD<7,
故答案为:2<AD<7;
(2)AC∥BQ,理由:由(1)知,△QDB≌△ADC,
∴∠BQD=∠CAD,
∴AC∥BQ;
(3)EF=2AD,AD⊥EF,
理由:如图2,延长AD到Q使得BQ=AD,连接BQ,
由(1)知,△BDQ≌△CDA(SAS),
∴∠DBQ=∠ACD,BQ=AC,
∵AC=AF,
∴BQ=AF,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴∠BAC+∠ABC+∠DBQ=180°,
∴∠BAC+ABQ=180°,
∵∠BAE=∠FAC=90°,
∴∠BAC+∠EAF=180°,
∴∠ABQ=∠EAF,
在△ABQ和△EAF中, ,
,
∴△ABQ≌△EAF,
∴AQ=EF,∠BAQ=∠AEF,
延长DA交EF于P,
∵∠BAE=90°,
∴∠BAQ+∠EAP=90°,
∴∠AEF+∠EAP=90°,
∴∠APE=90°,
∴AD⊥EF,
∵AD=DQ,
∴AQ=2AD,
∵AQ=EF,
∴EF=2AD,
即:EF=2AD,AD⊥EF.