题目内容

【题目】有4张相同的卡片分别写着数字﹣1、2、﹣3、4，将卡片的背面朝上，并洗匀．从中任意抽取1张，并将所取卡片上的数字记作一次函数y=kx+b中的k；再从余下的卡片中任意抽取1张，并将所取卡片上的数字记作一次函数y=kx+b中的b．则这个一次函数的图象恰好经过第一、二、四象限的概率是_______．

【答案】

【解析】

先根据这个一次函数图象经过第一、二、四象限得出，再利用列举法（画树状图）求概率即可得．

这个一次函数图象经过第一、二、四象限

则所求的问题转化为求第一次抽取卡片上的数字为负数，第二次抽取卡片上的数字为正数的概率

由题意，画树状图如下所示：

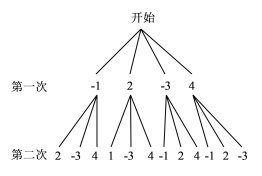
由此可知，两次抽取的所有可能的结果共有12种，它们每一种出现的可能性都相等，其中，第一次抽取卡片上的数字为负数，第二次抽取卡片上的数字为正数的结果有4种

则所求的概率为

故答案为：．

练习册系列答案
相关题目

【题目】为了解某区初中学生对网络游戏的喜好和作业量多少情况，随机抽取了该区500名同学进行了调查，并将调查的情况进行了整理，如下表：

作业量多少

网络游戏的喜好

认为作业多

认为作业不多

合计

喜欢网络游戏

180

90

270

不喜欢网络游戏

80

150

230

根据抽样调查结果，估计该区12000名初中生“不喜欢网络游戏并认为作业不多”的人数是________.

【题目】如图，为⊙的直径，点在的延长线上，点在⊙上，且．

(1)求证：是⊙的切线；

(2)已知，，点是的中点，，垂足为，交于点，求的长．

【题目】如图，抛物线y＝ax2+bx+2（a＜0）与x轴交于点A（﹣1，0）和点B（2，0），与y轴交于点C．

（1）求该抛物线的函数解析式；

（2）如图1，连接BC，点D是直线BC上方抛物线上的点，连接OD、CD，OD交BC于点F，当S△COF：S△CDF＝2：1时，求点D的坐标；

（3）如图2，点E的坐标为（0，﹣1），在抛物线上是否存在点P，使∠OBP＝2∠OBE？若存在，请直接写出符合条件的点P的坐标；若不存在，请说明理由．

【题目】某小学学生较多，为了便于学生尽快就餐，师生约定：早餐一人一份，一份两样，一样一个，食堂师傅在窗口随机发放（发放的食品价格一样），食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品．

（1）按约定，“小李同学在该天早餐得到两个油饼”是 事件；（可能，必然，不可能）

（2）请用列表或树状图的方法，求出小张同学该天早餐刚好得到猪肉包和油饼的概率．

【题目】某超市在疫情期间购进一批含75%酒精的消毒湿巾投放市场，则开始，由于消费者对此类产品认识不足，前几天的销量每况愈下；为了打开市场，提高销量，超市决定对该消毒湿巾打折销售，日销量每日增加，时间每增加1天，则日销量增加20包．超市工作人员对一个月（30天）销售情况进行了跟踪记录，并将记录情况绘成图像，图中的折线ABC表示该消毒湿巾日销量y(包)与销售时间x(天)之间的函数关系；

（1）第28天的日销售量是_______包；

（2）求y与x之间的函数关系式，并写出x的取值范围；

（3）若该产口进价为5元/包，AB段售价为15元/包，BC段在15元/包的基础上打a折销售，并且在30天中利润不低于3400元的天数有且只有10天，试确定a的最小值．

【题目】如图，抛物线经过点A（3，0），B（，0），与y轴交于点C，点P是抛物线在第四象限内的一点.

（1）求抛物线解析式；

（2）点D是线段OC的中点，OP⊥AD，点E是射线OP上一点，OE=AD，求DE的长；

（3）连接CP，AP，是否存在点P，使得OP平分四边形ABCP的面积？若存在，求点P的坐标；若不存在，说明理由.

【题目】如图，点是半圆的半径上的动点，作于．点是半圆上位于左侧的点，连结交线段于，且．

(1) 求证：是⊙O的切线．

(2) 若⊙O的半径为,,设．

①求关于的函数关系式．

②当时，求的值．

【题目】某小区新建成的住宅楼主体工程已经竣工，只剩下楼体外表需贴瓷砖，已知楼体外表的面积为．

（1）写出每块瓷砖的面积与所需的瓷砖块数（块）之间的函数关系式；

（2）为了使住宅楼的外观更漂亮，开发商决定采用灰、白、蓝三种颜色的瓷砖，每块瓷砖的面积都是，灰、白、蓝瓷砖使用比例是，则需要三种瓷砖各多少块？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网