ЬтФПФкШн
ЁОЬтФПЁПФГГЌЪадквпЧщЦкМфЙКНјвЛХњКЌ75%ОЦОЋЕФЯћЖОЪЊНэЭЖЗХЪаГЁЃЌдђПЊЪМЃЌгЩгкЯћЗбепЖдДЫРрВњЦЗШЯЪЖВЛзуЃЌЧАМИЬьЕФЯњСПУППігњЯТЃЛЮЊСЫДђПЊЪаГЁЃЌЬсИпЯњСПЃЌГЌЪаОіЖЈЖдИУЯћЖОЪЊНэДђелЯњЪлЃЌШеЯњСПУПШедіМгЃЌЪБМфУПдіМг1ЬьЃЌдђШеЯњСПдіМг20АќЃЎГЌЪаЙЄзїШЫдБЖдвЛИідТЃЈ30ЬьЃЉЯњЪлЧщПіНјааСЫИњзйМЧТМЃЌВЂНЋМЧТМЧщПіЛцГЩЭМЯёЃЌЭМжаЕФелЯпABCБэЪОИУЯћЖОЪЊНэШеЯњСПy(Аќ)гыЯњЪлЪБМфx(Ьь)жЎМфЕФКЏЪ§ЙиЯЕЃЛ
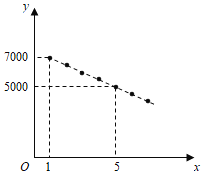
ЃЈ1ЃЉЕк28ЬьЕФШеЯњЪлСПЪЧ_______АќЃЛ
ЃЈ2ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєИУВњПкНјМлЮЊ5дЊ/АќЃЌABЖЮЪлМлЮЊ15дЊ/АќЃЌBCЖЮдк15дЊ/АќЕФЛљДЁЩЯДђaелЯњЪлЃЌВЂЧвдк30ЬьжаРћШѓВЛЕЭгк3400дЊЕФЬьЪ§гаЧвжЛга10ЬьЃЌЪдШЗЖЈaЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ420ЃЛЃЈ2ЃЉyЃН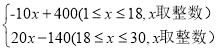 ЃЛЃЈ3ЃЉaЕФзюаЁжЕЮЊ9ЃЎ
ЃЛЃЈ3ЃЉaЕФзюаЁжЕЮЊ9ЃЎ
ЁОНтЮіЁП
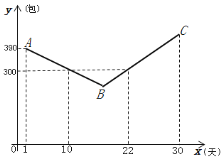
ЃЈ1ЃЉгЩЭМЯёПЩжЊЃЌBCЖЮКЏЪ§жаЃЌЕБxЃН22ЪБЃЌyЃН300ЃЛгЩЬтвтПЩжЊЃКУПдіМг1ЬьЃЌЯњСПдіМг20АќЃЌгЩДЫПЩвдМЦЫуГіЕк28ЬьЕФЯњЪлСПЃЛЃЈ2ЃЉНсКЯЭМЯёРћгУД§ЖЈЯЕЪ§ЗЈНјааЧѓНтЃЛЃЈ3ЃЉИљОнЬтвтСаВЛЕШЪННјаЮМЦЫу.
НтЃКЃЈ1ЃЉгЩЭМЯёПЩжЊЃЌBCЖЮКЏЪ§жаЃЌЕБxЃН22ЪБЃЌyЃН300ЃЛгЩЬтвтПЩжЊЃКУПдіМг1ЬьЃЌЯњСПдіМг20АќЃЌЫљвдЃЌЕБxЃН28ЪБЃЌyЃН300+(28-22)![]() 20=420.
20=420.
ЃЈ2ЃЉЩшABЖЮКЏЪ§НтЮіЪНЮЊyЃНkxЃЋbЃЎ
гЩЭМжЊЃКЕБxЃН1ЪБЃЌyЃН390ЃЛxЃН10ЃЌyЃН300ЃЎ
Ёр![]()
НтжЎЕУЃК![]()
ЁрABЖЮКЏЪ§НтЮіЪНЮЊЃКyЃН-10xЃЋ400
гЩЭМЯёПЩжЊЃЌBCЖЮКЏЪ§жаЃЌЕБxЃН22ЪБЃЌyЃН300ЃЛгЩЬтвтПЩжЊЃКУПдіМг1ЬьЃЌЯњСПдіМг20АќЃЌЫљвдЃЌЕБxЃН23ЪБЃЌyЃН320ЃЛПЩвдЧѓГіBCЖЮКЏЪ§НтЮіЪНЮЊЃКyЃН20x-140
ЛђепЃКгЩЬтвтПЩжЊЃКУПдіМг1ЬьЃЌЯњСПдіМг20АќЃЌЫљвдПЩСаГіКЏЪ§НтЮіЪНЮЊ
yЃН20ЃЈx-22ЃЉЃЋ300=20x-140
ЁОСНжжЗНЗЈЖМПЩвдЁП
Сю-10xЃЋ400=20x-140
НтжЎЕУЃКxЃН18
ЁрyЃН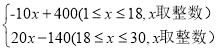
ЃЈ3ЃЉЕБ1ЁмxЁм18ЪБЃЌ
гЩ(15Ѓ5)yЁн3400ЕУЃЌ10(Ѓ10xЃЋ400)Ён3400ЃЌ
НтЕУЃКxЁм6ЃЎ
Ёр1ЁмxЁм6ЃЌxЃН1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6ЙВ6ЬьЃЎ
ЁпШеЯњЪлРћШѓВЛЕЭгк3400дЊЕФЬьЪ§гаЧвжЛга10ЬьЃЌ
ЁрЕБ18<xЁм30ЪБЃЌга4ЬьШеЯњЪлРћШѓВЛЕЭгк3600дЊЃЌ
гЩyЃН22x-140 (18<xЁм30)ЕУyЫцxЕФдіДѓЖјдіДѓЃЌ
ЁпxЮЊећЪ§ЃЌЁрxЃН27ЃЌ28ЃЌ29ЃЌ30ЪБЃЌШеЯњЪлРћШѓВЛЕЭгк3600дЊЃЌЧвЕБxЃН27ЪБЃЌРћШѓзюЕЭЃЎгЩЬтвтЕУЃЌ(15ЁС0ЃЎ1aЃ5)(20ЁС27-140)Ён3400ЃЎЁрaЁн9ЃЌ
ЁрaЕФзюаЁжЕЮЊ9ЃЎ

 ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ
ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИЁОЬтФПЁПЯТСаЪ§ОнЪЧМзЁЂввЁЂБћШ§ШЫИї10ТжЭЖРКЕФЕУЗжЃЈУПТжЭЖРК10ДЮЃЌУПДЮЭЖжаМЧ1ЗжЃЉЃК
БћЕУЗжЕФЦНОљЪ§гыжкЪ§ЖМЪЧ7ЃЌЕУЗжЭГМЦБэШчЯТЃК
ВтЪдађКХ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ЕУЗж | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
ЃЈ1ЃЉБћЕУЗжБэжаЕФa= ЃЌb= ЃЛ
ЃЈ2ЃЉШєдкЫћУЧШ§ШЫжабЁдёвЛЮЛЭЖРКЕУЗжИпЧвНЯЮЊЮШЖЈЕФЭЖЪжзїЮЊжїСІЃЌФуШЯЮЊбЁЫИќКЯЪЪЃПЧыгУФуЫљбЇЙ§ЕФЭГМЦжЊЪЖМгвдЗжЮіЫЕУїЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉМзЁЂввЁЂБћШ§ШЫЛЅЯржЎМфНјааДЋЧђСЗЯАЃЌУПИіШЫЕФЧђЖМЕШПЩФмЕФДЋИјЦфЫћСНШЫЃЌЧђзюЯШДгввЪжжаДЋГіЃЌОЙ§Ш§ДЮДЋЧђКѓЧђгжЛиЕНввЪжжаЕФИХТЪЪЧЖрЩйЃПЃЈгУЪїзДЭМЛђСаБэЗЈНтД№ЃЉ