题目内容
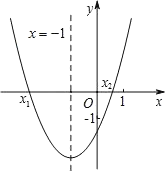
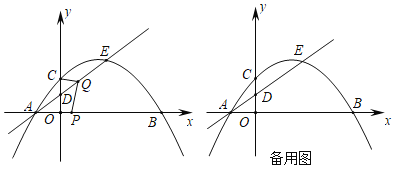
【题目】如图,抛物线![]() 经过点A(3,0),B(
经过点A(3,0),B(![]() ,0),与y轴交于点C,点P是抛物线在第四象限内的一点.
,0),与y轴交于点C,点P是抛物线在第四象限内的一点.
(1)求抛物线解析式;
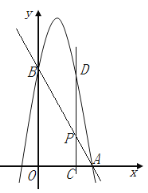
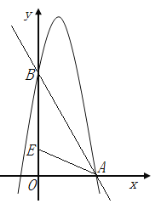
(2)点D是线段OC的中点,OP⊥AD,点E是射线OP上一点,OE=AD,求DE的长;
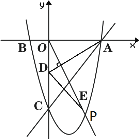
(3)连接CP,AP,是否存在点P,使得OP平分四边形ABCP的面积?若存在,求点P的坐标;若不存在,说明理由.

【答案】(1)![]() ,(2)
,(2)![]() ,(3)(
,(3)(![]() ,
,![]() )
)
【解析】
(1)抛物线的表达式为:![]() ,故
,故![]() ,解得:
,解得:![]() ,即可求解;
,即可求解;
(2)过E点作![]() 交OC于点
交OC于点![]() ,利用
,利用![]() 易证
易证![]() ,则可根据AAS证明
,则可根据AAS证明![]() 得到
得到![]() ,可得
,可得![]() 与
与![]() 点重合,则有
点重合,则有![]() ,得到
,得到![]() 是等腰直角三角形,可求得
是等腰直角三角形,可求得![]() ;
;
(3)根据OP平分四边形ABCP的面积,有![]() ,设P的横坐标为x,则纵坐标为:
,设P的横坐标为x,则纵坐标为:![]() ,得到
,得到![]() ,化简即可得出P点的坐标.
,化简即可得出P点的坐标.
解:(1)抛物线的表达式为:![]() ,
,
则有:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)过E点作![]() 交OC于点
交OC于点![]() ,
,
又(1)可知,抛物线的表达式为![]() ,
,
∴C的坐标为:(0,-3),
∴![]() ,
,
∵![]() ,
,
∴![]()
∵![]()
∴![]()
在![]() 和
和![]() 中
中
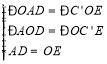
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() 与
与![]() 点重合,
点重合,
∴![]()
又∵点D是线段OC的中点,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ;
;
(3)答:存在点P,使得OP平分四边形ABCP的面积.
证明:设P的横坐标为x,则纵坐标为:![]() ,
,
根据OP平分四边形ABCP的面积,
有:![]() ,
,
即:![]()
∴![]()
解之得:![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴纵坐标为:![]() ,
,
∴P的坐标为:(2,-3).

练习册系列答案
相关题目