题目内容
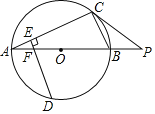
【题目】如图,![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在⊙
在⊙![]() 上,且
上,且![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)已知![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)EF=![]() .
.
【解析】
(1)连接OC,由AB是直径,可得∠ACB=90°,再由OA=OC,可得∠CAO=∠ACO,证明△PBC∽△PCA,可得∠PCB=∠CAO,继而可得∠OCP=90°,由此即可得结论;
(2)连接OD,先求出PA=40,然后求出OA=15,由点![]() 是
是![]() 的中点,则可得∠FOD=90°,由△PBC∽△PCA,可得
的中点,则可得∠FOD=90°,由△PBC∽△PCA,可得![]() ,证明△AEF∽△ACB,可得
,证明△AEF∽△ACB,可得![]() ,即AE=2EF,证明△DOF∽△AEF,可得
,即AE=2EF,证明△DOF∽△AEF,可得![]() ,从而求出OF=
,从而求出OF=![]() ,进而求出AF=
,进而求出AF=![]() ,在Rt△AEF中,利用勾股定理求出EF长即可.
,在Rt△AEF中,利用勾股定理求出EF长即可.
(1)连接OC,
∵AB是直径,
∴∠ACB=90°,即∠ACO+∠OCB=90°,
∵OA=OC,
∴∠CAO=∠ACO,
∵![]() ,
,
∴![]() ,
,
又∵∠P=∠P,
∴△PBC∽△PCA,
∴∠PCB=∠CAO,
∴∠PCB+∠OCB=90°,即∠OCP=90°,
∴PC是⊙O的切线;

(2)连接OD,
∵![]() ,
,![]() ,
,![]() ,
,
∴PA=40,
∴AB=PA-PC=30,
∴OA=15,
∵点![]() 是
是![]() 的中点,AB是直径,
的中点,AB是直径,
∴OD=OA=15,DO⊥AB,即∠FOD=90°,
∵△PBC∽△PCA,
∴![]() ,
,
∵∠AEF=∠ACB=90°,∠A=∠A,
∴△AEF∽△ACB,
∴![]() ,即AE=2EF,
,即AE=2EF,
∵∠AEF=∠DOF=90°,∠AFE=∠DFO,
∴△DOF∽△AEF,
∴![]() ,
,
∴OF=![]() OD=
OD=![]() ,
,
∴AF=AO-OF=![]() ,
,
在Rt△AEF中,AF2=AE2+EF2,
即(![]() )2=(2EF)2+EF2,
)2=(2EF)2+EF2,
∴EF=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目