Question

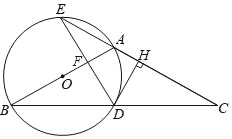
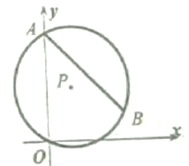
【题目】如图，已知点经过原点，交轴正半轴于点．点在上，，圆心的坐标为__________．

Answer 1

【答案】

【解析】

连接OP，OB，PB，延长BP交⊙P于E，连接OE，作EF⊥OA于F，BH⊥x轴于H.利用全等三角形的性质求出点E坐标即可解决问题.

解：连接OP，OB，PB，延长BP交⊙P于E，连接OE，作EF⊥OA于F，BH⊥x轴于H．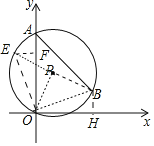

∵∠BPO=2∠BAO，∠BAO=45°，
∴∠BPO=90°，
∵PO=OB，
∴△PBO是等腰直角三角形，
∵BE是直径，
∴∠BOE=90°，
∴∠OBE=∠OEB=45°，
∴OE=OB，
∵∠EOB=∠AOH=90°，
∴∠EOF=∠BOH，
∵∠EFO=∠BHO=90°，
∴△EFO≌△BHO(AAS)，
∴OF=OH=5，EF=BH=2，
∴E(2,5)，
∵PE=PB，
∴P.
故答案为.