题目内容
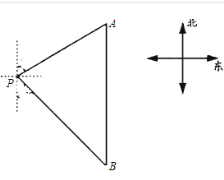
【题目】如图，在△ABC中，AB＝AC，以为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．
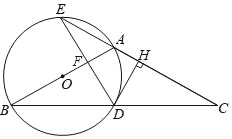
（1）求证：DH是圆O的切线；
（2）若
＝
，求证A为EH的中点；
（3）若EA＝EF＝2，求圆O的半径．
【答案】（1）见解析；（2）见解析；（3）⊙O的半径为1+
【解析】
（1）根据同圆的半径相等和等边对等角证明∠ODB＝∠OBD＝∠ACB，则DH⊥AC，则DH是圆O的切线；
（2）先证明∠E＝∠B＝∠C，得△EDC是等腰三角形，证明△AEF∽△ODF，则
，设OD＝3x，AE＝2x，可知EC＝8x，根据等腰三角形三线合一得EH＝CH＝4x，从而得结论；
（3）设⊙O的半径为r，即OD＝OB＝r，证明DF＝OD＝r，则DE＝DF+EF＝r+2，BD＝CD＝DE＝r+2，证明△BFD∽△EFA，列比例式为
，列方程即可求出r的值．
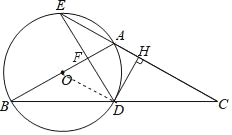
（1）证明：连接OD，如图，
∵OB＝OD，
∴△ODB是等腰三角形，
∠OBD＝∠ODB①，
在△ABC中，∵AB＝AC，
∴∠ABC＝∠ACB②，
由①②得：∠ODB＝∠OBD＝∠ACB，
∴OD∥AC，
∵DH⊥AC，
∴DH⊥OD，
∴DH是圆O的切线；
（2）解：如图，在⊙O中，∵∠E＝∠B，
∴由（1）可知：∠E＝∠B＝∠C，
∴△EDC是等腰三角形，
∵
∵AE∥OD，
∴△AEF∽△ODF，
∴
设OD＝3x，AE＝2x，
∵AO＝BO，OD∥AC，
∴BD＝CD，
∴AC＝2OD＝6x，
∴EC＝AE+AC＝2x+6x＝8x，
∵ED＝DC，DH⊥EC，
∴EH＝CH＝4x，
∴AH＝EH﹣AE＝4x﹣2x＝2x，
∴AE＝AH，
∴A是EH的中点；
（3）解：如图，设⊙O的半径为r，即OD＝OB＝r，
∵EF＝EA，
∴∠EFA＝∠EAF，
∵OD∥EC，
∴∠FOD＝∠EAF，
则∠FOD＝∠EAF＝∠EFA＝∠OFD，
∴DF＝OD＝r，
∴DE＝DF+EF＝r+2，
∴BD＝CD＝DE＝r+2，
在⊙O中，∵∠BDE＝∠EAB，
∴∠BFD＝∠EFA＝∠EAB＝∠BDE，
∴BF＝BD，△BDF是等腰三角形，
∴BF＝BD＝r+2，
∴AF＝AB﹣BF＝2OB﹣BF＝2r﹣（2+r）＝r﹣2，
∵∠BFD＝∠EFA，∠B＝∠E，
∴△BFD∽△EFA，
∴
∴
解得：r1＝1+，r2＝1﹣（舍），
经检验地，r＝1+时，
，故根成立
综上所述，⊙O的半径为1+．
