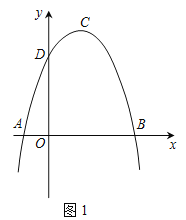题目内容
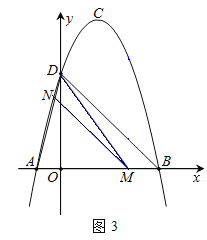
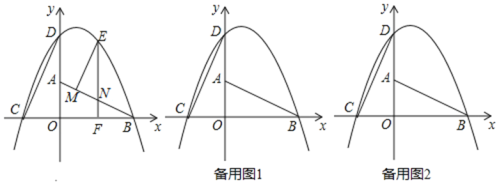
【题目】已知抛物线![]() ,通过画图发现,无论
,通过画图发现,无论![]() 取何值,抛物线总会经过两个定点
取何值,抛物线总会经过两个定点
![]() 直接写出这两个定点的坐标 、 ;
直接写出这两个定点的坐标 、 ;
![]() 若将此抛物线向右平移
若将此抛物线向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
![]() 若抛物线
若抛物线![]() 与直线
与直线![]() 有两个交点
有两个交点![]() 与
与![]() .且
.且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)抛物线![]() =b(x2+x)-3x-3,函数过定点,则x2+x=0,即可求解;
=b(x2+x)-3x-3,函数过定点,则x2+x=0,即可求解;
(2)原抛物线顶点坐标为(![]() ,
,![]() ),平移后为(
),平移后为(![]() ,
,![]() ),即可求解;
),即可求解;
(3)由![]() ,则1≤AB两点水平距离≤4,分当b>0时和当b<0时用韦达定理即可求解.
,则1≤AB两点水平距离≤4,分当b>0时和当b<0时用韦达定理即可求解.
解(1)∵![]() =b(x2+x)-3x-3, 函数过定点,
=b(x2+x)-3x-3, 函数过定点,
∴x2+x=0,解得,x=0或x=-1,
∴抛物线总会经过![]()
故答案为![]() ;
;
![]() 解:原抛物线顶点横坐标为:
解:原抛物线顶点横坐标为:![]()
纵坐标为:![]()
平移后新抛物线顶点横坐标为:![]()
纵坐标为:![]()
由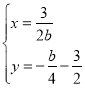
得:![]()
即为平移后的抛物线顶点所在的函数解析式.
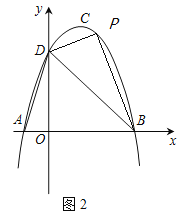
(3)∵![]() ,则1≤AB两点水平距离≤4,
,则1≤AB两点水平距离≤4,
当b>0时,
设抛物线与直线交点为A与B,则A(0,-3),B(x,y),
∴![]() =x-3,整理得,bx2+(b-4)x=0,
=x-3,整理得,bx2+(b-4)x=0,
由韦达定理得,x+0=![]() ,则1≤
,则1≤![]() ≤4,
≤4,
解得:![]() ≤b≤2,
≤b≤2,
同理,当b<0时,解得:![]()
综上所述,![]() 的取值范围为
的取值范围为![]() 或
或![]()

练习册系列答案
相关题目