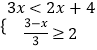Question

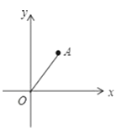
【题目】如图，平面直角坐标系内有一点A（1，1），O为坐标原点．点B在x轴上，且构成的△AOB为等腰三角形，则符合条件的点B有_______个．

Answer 1

【答案】4

【解析】

根据点A的坐标为（1，1），得到OA=，当OA是底边时，当OA是腰，O是顶角顶点时，当OA是腰，A是顶角顶点时，即可得到结论．

解：

∵点A的坐标为（1，1），

∴OA=，

当OA是底边时，B在线段OA的中垂线上，与x轴有1个交点，则B1（1，0）；

当OA是腰，O是顶角顶点时，B是以O为圆心，以OA为半径的圆与x轴的交点，共有2个点，则B2（-，0），B3（，0）；

当OA是腰，A是顶角顶点时，B是以A为圆心，以OA为半径的圆与x轴的交点，除去原点O以外有1个点，则B4（2，0）；

∴满足条件的点B的坐标为（1，0）或（-，0）或（，0）或（2，0）；

故答案为：4．