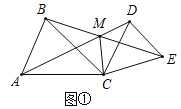
题目内容
【题目】如图1,![]() ,
,![]() ,
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如图2,当
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 为等腰直角三角形,证明见解析.
为等腰直角三角形,证明见解析.
【解析】
分析(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CAD=∠CBE,再根据∠AFC=∠BFH,即可得到∠AMB=∠ACB=α;
(3)先根据SAS判定△ACP≌△BCQ,再根据全等三角形的性质,得出CP=CQ,∠ACP=∠BCQ,最后根据∠ACB=90°即可得到∠PCQ=90°,进而得到△PCQ为等腰直角三角形.
![]() 如图1,
如图1,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
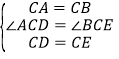 ,
,
![]() ≌
≌![]()
![]() ;
;
![]() 如图1,
如图1,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() 中,
中,![]() ;
;
![]() 为等腰直角三角形.
为等腰直角三角形.
证明:如图2,由![]() 可得,
可得,![]() ,
,
![]() ,BE的中点分别为点P、Q,
,BE的中点分别为点P、Q,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
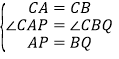 ,
,
![]() ≌
≌![]() ,
,
![]() ,且
,且![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形.
为等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目