题目内容
【题目】如图1,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形如图2.
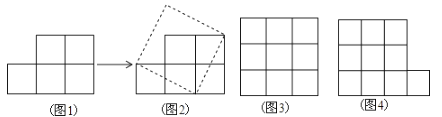
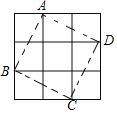
(1)你能在![]() 方格图(图3)中,连接四个格点(网格线的交点)组成面积为5的正方形吗?若能,请用虚线画出.
方格图(图3)中,连接四个格点(网格线的交点)组成面积为5的正方形吗?若能,请用虚线画出.
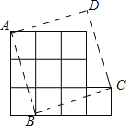
(2)你能把十个小正方形组成的图形纸(图4),剪开并拼成正方形吗?若能,请仿照图2的形式把它重新拼成一个正方形.
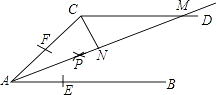
(3)如图,是由两个边长不等的正方形纸片组成的一个图形,要将其剪拼成一个既不重叠也无空隙的大正方形,则剪出的块数最少为________块.请你在图中画出裁剪线,并说明拼接方法.
【答案】(1)能,作图见解析;(2)能,作图见解析;(3)5,作图及说明见解析
【解析】
(1)画出边长为![]() 的正方形即可;
的正方形即可;
(2)结合例题,画出边长为![]() 的正方形即可;
的正方形即可;
(3)在AB上截取AM=BE,连接DM、MF,然后拼成大正方形即可.
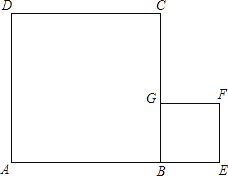
解:(1)能,如图所示,正方形ABCD即为所求;
(2)能,如图所示,正方形ABCD即为所求;
(3)如图所示,
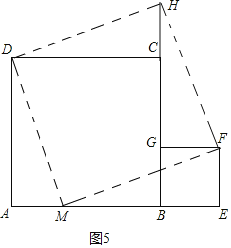
在AB上截取AM=BE,连接DM、MF,
DM、FM即为裁剪线,
将△DAM拼接△DCH处,使DA与DC重合,将△MEF拼接至△HGF处,使ME和HG重合,EF与FG重合,得到正方形DMFH,
∴剪出的块数最少为5块,
故答案为:5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目