题目内容
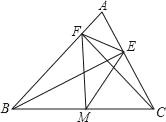
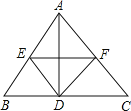
【题目】如图所示,在△ABC中,AD⊥BC于D,DE∥AC于E,DF∥AB交AC于F,连接EF。
(1)当△ABC满足什么条件时,四边形AEDF是矩形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形,并说明理由。
【答案】(1)∠BAC=90°,理由见解析;(2)∠BAC=90°,且AB=AC,理由见解析
【解析】
试题(1)先由已知条件证出四边形![]() 是平行四边形,再由
是平行四边形,再由![]() 即可得出四边形
即可得出四边形![]() 是矩形;
是矩形;
(2)由(1)得:当![]() 时,四边形
时,四边形![]() 是矩形,再证出
是矩形,再证出![]() 即可得出四边形
即可得出四边形![]() 是正方形.
是正方形.
试题解析:(1)当△ABC满足∠BAC=90时,四边形AEDF是矩形;理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
又![]()
∴四边形AEDF是矩形;
(2)当△ABC满足![]() ,且AB=AC时,四边形AEDF是正方形;理由如下:
,且AB=AC时,四边形AEDF是正方形;理由如下:
由(1)得:当![]() 时,四边形AEDF是矩形,
时,四边形AEDF是矩形,
又∵AB=AC,
![]()
∵AD⊥BC,
∴△ABD和△ACD是等腰直角三角形,
∵DE∥AC,
∴DE⊥AB,
∴AE=BE,
![]() 同理:
同理:![]()
∴DE=DF,
∴四边形AEDF是正方形;

练习册系列答案
相关题目