Question

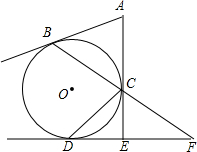
如图所示，AC为⊙O的直径且PA⊥AC，BC是⊙O的一条弦，直线PB交直线AC于点D，

DB

DP

=

DC

DO

=

2

3

．
（1）求证：直线PB是⊙O的切线；
（2）求cos∠BCA的值．

Answer 1

（1）证明：连接OB、OP，如图，
∵

DB

DP

=

DC

DO

=

2

3

，且∠D=∠D，
∴△BDC∽△PDO，
∴∠DBC=∠DPO，
∴BC∥OP，
∴∠BCO=∠POA，∠CBO=∠BOP
而OB=OC
∴∠OCB=∠CBO
∴∠BOP=∠POA
又∵OB=OA，OP=OP
∴△BOP≌△AOP
∴∠PBO=∠PAO
又∵PA⊥AC
∴∠PBO=90°
∴直线PB是⊙O的切线；

（2）由（1）知∠BCO=∠POA，
设PB=a，则BD=2a
又∵PA=PB=a
∴AD=

DP2-PA2

=2

2

a，
又∵BC∥OP
∴DC=2CO，
∴DC=CA=

1

2

×2

2

a=

2

a，
∴OA=

2

2

a，
∴OP=

OA2+PA2

=

( 2 a 2 )2+a2

=

6

2

a，
∴cos∠BCA=cos∠POA=

OA

OP

=

3

3

．