题目内容
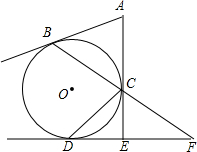
如图，AC为⊙O直径，B为AC延长线上的一点，BD交⊙O于点D，∠BAD=∠B=30°
（1）求证：BD是⊙O的切线；
（2）请问：BC与BA有什么数量关系？写出这个关系式，并说明理由．
（1）求证：BD是⊙O的切线；
（2）请问：BC与BA有什么数量关系？写出这个关系式，并说明理由．
（1）证明：连接OD，
∵OD=OA，
∴∠OAD=∠ODA=30°，
∴∠DOB=60°；
又∵∠DBA=30°，
∴∠ODB=90°，
∵D为⊙O上一点，
∴BD是⊙O的切线．
（2）BC=
AB．理由如下：
连接CD；
∵OD=OC且∠DOB=60°，
∴△ODC为等边三角形，
∴∠DOC=60°，
∴OD=
OB；
∵OA=OD=OC，
∴BC=OB-OC，
∴BC=
AB．
∵OD=OA，
∴∠OAD=∠ODA=30°，
∴∠DOB=60°；
又∵∠DBA=30°，
∴∠ODB=90°，
∵D为⊙O上一点，
∴BD是⊙O的切线．
（2）BC=
| 1 |
| 3 |
连接CD；
∵OD=OC且∠DOB=60°，
∴△ODC为等边三角形，
∴∠DOC=60°，
∴OD=
| 1 |
| 2 |
∵OA=OD=OC，
∴BC=OB-OC，
∴BC=
| 1 |
| 3 |
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
DE于点F．若BC=24，sin∠F=
