Question

【题目】在平面直角坐标系xOy中，点M的坐标为（x1，y1），点N的坐标为（x2，y2），且x1≠x2，y1≠y2，以MN为边构造菱形，若该菱形的两条对角线分别平行于x轴，y轴，则称该菱形为边的“坐标菱形”．

（1）已知点A（2，0），B（0，2），则以AB为边的“坐标菱形”的最小内角为　 　；

（2）若点C（1，2），点D在直线y=5上，以CD为边的“坐标菱形”为正方形，求直线CD 表达式；

（3）⊙O的半径为，点P的坐标为（3，m）．若在⊙O上存在一点Q，使得以QP为边的“坐标菱形”为正方形，求m的取值范围．

Answer 1

【答案】（1）60°；（2）y=x+1或y=﹣x+3；（3）1≤m≤5或﹣5≤m≤﹣1

【解析】分析：（1）根据定义建立以AB为边的“坐标菱形”，由勾股定理求边长AB=4，可得30度角，从而得最小内角为60°；

（2）先确定直线CD与直线y=5的夹角是45°，得D（4，5）或（﹣2，5），易得直线CD的表达式为：y=x+1或y=﹣x+3；

（3）分两种情况：

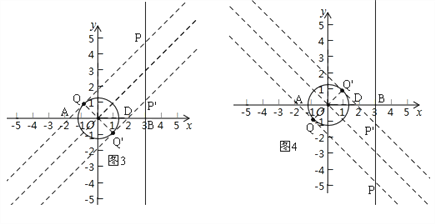
①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3，根据等腰直角三角形的性质分别求P'B=BD=1，PB=5，写出对应P的坐标；

②先作直线y=﹣x，再作圆的两条切线，且平行于直线y=﹣x，如图4，同理可得结论．

详解：（1）∵点A（2，0），B（0，2），∴OA=2，OB=2．在Rt△AOB中，由勾股定理得：AB==4，∴∠ABO=30°．

∵四边形ABCD是菱形，∴∠ABC=2∠ABO=60°．

∵AB∥CD，∴∠DCB=180°﹣60°=120°，∴以AB为边的“坐标菱形”的最小内角为60°．

故答案为：60°；

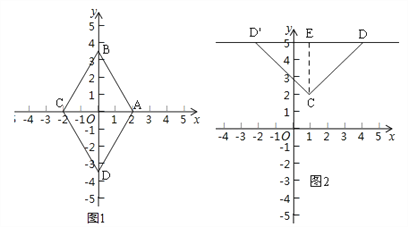
（2）如图2．

∵以CD为边的“坐标菱形”为正方形，∴直线CD与直线y=5的夹角是45°．

过点C作CE⊥DE于E，∴D（4，5）或（﹣2，5），∴直线CD的表达式为：y=x+1或y=﹣x+3；

（3）分两种情况：

①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3．

∵⊙O的半径为，且△OQ'D是等腰直角三角形，∴OD=OQ'=2，∴P'D=3﹣2=1．

∵△P'DB是等腰直角三角形，∴P'B=BD=1，∴P'（0，1），同理可得：OA=2，∴AB=3+2=5．

∵△ABP是等腰直角三角形，∴PB=5，∴P（0，5），∴当1≤m≤5时，以QP为边的“坐标菱形”为正方形；

②先作直线y=﹣x，再作圆的两条切线，且平行于直线y=﹣x，如图4．

∵⊙O的半径为，且△OQ'D是等腰直角三角形，∴OD=OQ'=2，∴BD=3﹣2=1．

∵△P'DB是等腰直角三角形，∴P'B=BD=1，∴P'（0，﹣1），同理可得：OA=2，∴AB=3+2=5．

∵△ABP是等腰直角三角形，∴PB=5，∴P（0，﹣5），∴当﹣5≤m≤﹣1时，以QP为边的“坐标菱形”为正方形；

综上所述：m的取值范围是1≤m≤5或﹣5≤m≤﹣1．