��Ŀ����
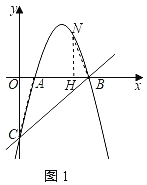
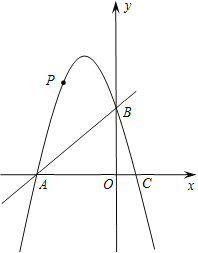
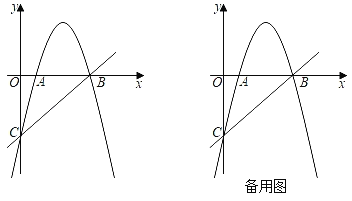
����Ŀ����ͼ��������y��ax2+6x+c��x����A��B���㣬��y���ڵ�C��ֱ��y��x��5������B��C��
��1���������ߵĽ���ʽ��
��2������NΪ�������϶��㣬����NBA����OACʱ�����N�����꣬
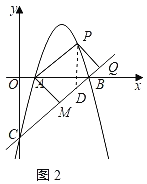
��3������A��ֱ�߽�ֱ��BC�ڵ�M����AM��BCʱ������������һ����P�������B��C�غϣ�����ֱ��AM��ƽ���߽�ֱ��BC�ڵ�Q�����Ե�A��M��Q��PΪ������ı�����ƽ���ı��Σ����P�ĺ����꣮
���𰸡���1��y����x2+6x��5����2��N������Ϊ����4����45������3����P�ĺ�����Ϊ4��![]() ��
��![]() ��
��
��������
��1�������C��0����5����B��5��0��������y��ax2+6x+c��a��c��ֵ�����ɵó������
��2�����A��1��0�����ó�OA��1��OC��5����������������һ��N��NH��x���ڵ�H������AC��BN���ɡ�OAC����ǣ���N��ĺ�����С��5����֤��NBH����CAO���ó�![]() ����N������Ϊ��n����n2+6n��5������NH��|��n2+6n��5|��BH��|5��n|���ó�
����N������Ϊ��n����n2+6n��5������NH��|��n2+6n��5|��BH��|5��n|���ó� �����n��ֵ���ɵó������
�����n��ֵ���ɵó������
��3��֤����OCB����AMB��Ϊ����ֱ�������Σ���AM��![]() AB��
AB��![]() ����ƽ���ı��ε����ʵó�AM//PQ��PQ��AM��
����ƽ���ı��ε����ʵó�AM//PQ��PQ��AM��![]() ���Ƴ�PQ��BC����PD��x�ύֱ��BC��D����ƽ���ߵ����ʵó���PDQ����OCB��45��������DPQ�ǵ���ֱ�������Σ��ó�PD��
���Ƴ�PQ��BC����PD��x�ύֱ��BC��D����ƽ���ߵ����ʵó���PDQ����OCB��45��������DPQ�ǵ���ֱ�������Σ��ó�PD��![]() PQ��4����P��m����m2+6m��5������D��m��m��5��������P��ֱ��BC�Ϸ�ʱ��PD����m2+5m��4���ⷽ�̼��ɣ�����P��ֱ��BC�·�ʱ��PD��m2��5m��4���ⷽ�̼��ɵó������
PQ��4����P��m����m2+6m��5������D��m��m��5��������P��ֱ��BC�Ϸ�ʱ��PD����m2+5m��4���ⷽ�̼��ɣ�����P��ֱ��BC�·�ʱ��PD��m2��5m��4���ⷽ�̼��ɵó������
�⣺��1����x��0ʱ��y��x��5����5��
��C��0����5����
��y��0ʱ��x��5��0��
��ã�x��5��
��B��5��0����
��B��5��0����C��0����5������y��ax2+6x+c�ã�![]() ��
��
��ã� ![]() ��
��
�������߽���ʽΪy����x2+6x��5��
��2���x2+6x��5��0����ã�x1��1��x2��5��
��A��1��0����
��C��0����5����
��OA��1��OC��5��
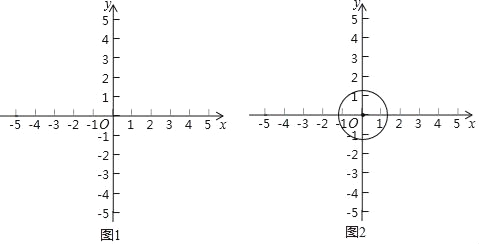
��������������һ��N��NH��x���ڵ�H������AC��BN����ͼ1��ʾ��
�ߡ�OAC����ǣ�
��N��ĺ�����С��5��
�ߡ�NBA����OAC����NHB��90������AOC��
���NBH����CAO��
��![]() ��
��
��N��������n����n2+6n��5����
��NH��|��n2+6n��5|��BH��|5��n|��
�� ��
��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��
��ã�n1��5����ȥ����n2��6����ȥ����
��![]() ʱ��
ʱ��
��ã�n1��5����ȥ����n2����4��
��n����4ʱ����n2+6n��5����45��
��N����4����45����
����������N����������4����45����
��3����A��1��0����B��5��0����C��0����5����
��AB��4����OCBΪ����ֱ�������Σ�
���OBC����OCB��45����
��AM��BC��
���AMBΪ����ֱ�������Σ�
��AM��![]() AB��
AB��![]() ��4��
��4��![]() ��
��
���Ե�A��M��Q��PΪ������ı�����ƽ���ı��Σ�
��AM//PQ��PQ��AM��![]() ��
��
��PQ��BC��
��PD��x�ύֱ��BC��D����ͼ2��ʾ��
���PDQ����OCB��45����
���DPQ�ǵ���ֱ�������Σ�
��PD��![]() PQ��
PQ��![]() ��
��
��P��m����m2+6m��5������D��m��m��5����
����P��ֱ��BC�Ϸ�ʱ��PD����m2+6m��5����m��5������m2+5m��4��
���m1��1����ȥ����m2��4��
����P��ֱ��BC�·�ʱ��PD��m��5������m2+6m��5����m2��5m��4��
��ã�m1��![]() ��m2��
��m2��![]() ��
��
������������P�ĺ�����Ϊ4��![]() ��
��![]() ��
��