题目内容
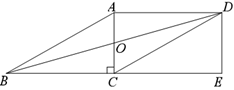
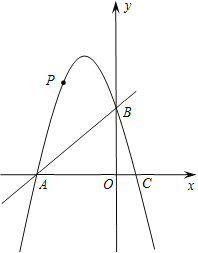
【题目】(阅读理解)设点P在矩形ABCD内部,当点P到矩形的一条边的两个端点距离相等时,称点P为该边的“和谐点”.例如:如图1,矩形ABCD中,若PA=PD,则称P为边AD的“和谐点”.
(解题运用)已知,点P在矩形ABCD内部,且AB=10,BC=6.
(1)设P是边AD的“和谐点”,则P 边BC的“和谐点”(填“是”或“不是”);
(2)若P是边BC的“和谐点”,连接PA,PB,当△PAB是直角三角形时,求PA的值;
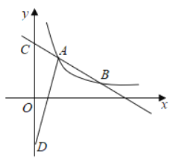
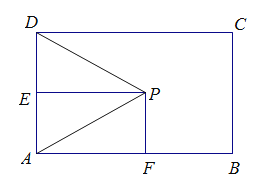
(3)如图2,若P是边AD的“和谐点”,连接PA,PB,PD,求tan∠PAB· tan∠PBA的最小值.
【答案】(1)是;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)证明△PAB≌△PDC,即可得证;
(2)先得出P在AD和BC的垂直平分线上,过P作PE⊥AD于E,PF⊥AB于F,易证四边形PEAF为矩形,可得PF=3,根据PF⊥AB,得出PF2=AF·(AB-AF),设AF=x,解得x1=1,x2=9,然后即可得出答案;
(3)作PF⊥AB于F,由(2)可知PF=3,可得tan∠PAB·tan∠PBA=![]() =
=![]() ,设AF=x,则BF=10-x,可得AF·BF=(10-x)·x,可求出AF·BF的最大值,即可推出
,设AF=x,则BF=10-x,可得AF·BF=(10-x)·x,可求出AF·BF的最大值,即可推出![]() 的最小值.
的最小值.
(1)是;
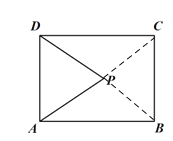
连接PB,PC
∵P是边AD的“和谐点”,
∴PA=PD,
∴∠PDA=∠PAD,
∵∠CDA=∠BAD=90°,
∴∠CDP=∠BAP,
∵AP=DP,AB=CD,
∴△PAB≌△PDC(SAS),
∴PB=PC;
(2)∵P是BC的和谐点,
∴P也是AD的和谐点,
∴PB=PC,PA=PD,
∴P在AD和BC的垂直平分线上,
过P作PE⊥AD于E,PF⊥AB于F,
易证四边形PEAF为矩形,
∴PF=AE,
又∵PA=PD,PE⊥AD,
∴AE=![]() AD=3,
AD=3,
∴PF=3,
又∵△ABP为直角三角形,且P在矩形内部,
∴只能∠APB=90°,
又∵PF⊥AB,
∴PF2=AF·BF(射影定理),
∴PF2=AF·(AB-AF),
设AF=x,
∴x(10-x)=9,
x2-10x+9=0,
(x-1)(x-9)=0,
∴x1=1,x2=9,
当AF=9时 PA=![]() =
=![]() ,
,
AF=1时 PA=![]() =
=![]() ,
,
∴AF的值为![]() 或
或![]() ;
;
(3)作PF⊥AB于F,由(2)可知PF=3,

∴tan∠PAB=![]() ,tan∠PBA=
,tan∠PBA=![]() ,
,
∴tan∠PAB·tan∠PBA=![]() =
=![]()
设AF=x,则BF=10-x,
∴AF·BF=(10-x)·x=-x2+10x=-(x-5)2+25,
当x=5时,AF·BF有最大值25,
∴![]() 有最小值是
有最小值是![]() ,
,
∴tan∠PAB·tan∠PBA的最小值是![]() .
.