Question

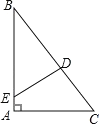
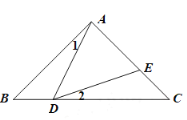
【题目】如图，在等腰三角形ABC中，∠BAC=90°，AB=AC=2，D是BC边上的一个动点，（不与B、C重合）在AC边上取一点E，使∠ADE=45°．

（1）求证：△ABD∽△DCE；

（2）设BD=x，AE=y．

①求y关于x的函数关系式并写出自变量x的取值范围；

②求y的最小值．

Answer 1

【答案】（1）见解析；（2）①，②1

【解析】

（1）根据等腰直角三角形的性质得到∠B＝∠C＝45°，根据三角形的外角性质得到∠BAD＝∠EDC，根据相似三角形的判定定理证明结论；

（2）①根据相似三角形的性质列出比例式，代入计算得到y关于x的函数关系式；

②根据二次函数的性质计算即可．

（1）证明：∵∠BAC=90°，AB=AC，

∴∠B=∠C=45°．

∵∠ADC=∠B+∠1=45°+∠1，∠ADC=∠ADE+∠2=45°+∠2，

∴∠1=∠2．

∴△ABD∽△DCE．

（2）解：①∵△ABD∽△DCE，

∴．

∵AB=AC=2，BD=x，AE=y，

∴，，．

∴．

∴．

② ∵，

∴y的最小值是1．